九九热视频精品在线_国产成人mv视频在线观看_国产精品三级一区二区_亚洲精品国产av成拍色拍婷婷_久久伊人一区二区_国产高清精品网站_九九99热久久精品离线6_国产在线一卡2卡三卡4卡免费_日韩美女乱淫aaa高清视频_亚洲大胆_啪啪一级视频_午夜av免费观看_国产高清精品福利私拍国产写真_亚洲婷婷五月综合狠狠_日韩欧美一区二区三区视频_岛国av免费看_精品国产乱码久久久久久久软件_亚洲国产成人精品无码区99_www日本色_免费黄色看片

大家好，這是我們翻譯的西瓜書(shū)平替。

「小白學(xué) AI 該從哪里下手？」

去互聯(lián)網(wǎng)上搜索一圈，最高贊的回復(fù)往往是高數(shù)起手，概率論也要學(xué)一學(xué)吧，再推薦一本大名鼎鼎的「西瓜書(shū)」。

但入門(mén)的門(mén)檻足以勸退一大波人了。翻開(kāi)《西瓜書(shū)》前幾頁(yè)，看看基本術(shù)語(yǔ)解釋?zhuān)恍┗緮?shù)學(xué)概念還是要了解的。

西瓜書(shū)《機(jī)器學(xué)習(xí)》第 3 頁(yè)。

但為了避免「從入門(mén)到放棄」，有沒(méi)有一種可能，不需要學(xué)更多數(shù)學(xué)，就能搞懂大模型的運(yùn)行原理？

最近，Meta Gen AI 部門(mén)的數(shù)據(jù)科學(xué)總監(jiān) Rohit Patel 聽(tīng)到了你的心聲。他用加法和乘法 —— 小學(xué)二年級(jí)的數(shù)學(xué)知識(shí)，深入淺出地解析了大模型的基礎(chǔ)原理。

原文鏈接：https://towardsdatascience.com/understanding-llms-from-scratch-using-middle-school-math-e602d27ec876

如果你想更進(jìn)一步，按照博客中的指導(dǎo)，親手構(gòu)建一個(gè)像 Llama 系列的 LLM 也完全可行。

讀過(guò)的網(wǎng)友留下了好評(píng)：「博客相當(dāng)長(zhǎng)，雖然我才看了一半，但可以向你保證，這值得花時(shí)間一讀。」

「所有的知識(shí)點(diǎn)都包圓了，學(xué)這 1 篇頂 40 億篇其他資料！」

內(nèi)容概覽

為了使內(nèi)容更簡(jiǎn)潔，Rohit 盡量避免了機(jī)器學(xué)習(xí)領(lǐng)域的復(fù)雜術(shù)語(yǔ)，將所有概念簡(jiǎn)化為了數(shù)字。

整個(gè)博客首先回答了四個(gè)問(wèn)題：

一個(gè)簡(jiǎn)單的神經(jīng)網(wǎng)絡(luò)怎樣構(gòu)成？這些模型是如何訓(xùn)練的？這一切是如何生成語(yǔ)言的？是什么讓 LLM 的性能如此出色？

在基礎(chǔ)的原理摸清之后，Rohit 要從細(xì)節(jié)入手，從嵌入、分詞器、自注意力等概念講起，由淺入深，逐步過(guò)渡到對(duì) GPT 和 Transformer 架構(gòu)的全面理解。

這個(gè)博客對(duì)新手有多友好呢？先來(lái)試讀一段：

神經(jīng)網(wǎng)絡(luò)只能接受數(shù)字輸入，并且只能輸出數(shù)字，沒(méi)有例外。關(guān)鍵在于如何將各種形式的輸入轉(zhuǎn)換為數(shù)字，以及如何將輸出的數(shù)字解讀為所需的結(jié)果。從本質(zhì)上講，構(gòu)建 LLM 的核心問(wèn)題就是設(shè)計(jì)一個(gè)能夠執(zhí)行這些轉(zhuǎn)換的神經(jīng)網(wǎng)絡(luò)。

那么一個(gè)可以根據(jù)圖片輸入，分出花朵和葉子的神經(jīng)網(wǎng)絡(luò)大概是這樣的：

其中，RGB 值表示圖像的顏色信息，Vol 則表示圖像中物體的尺寸

神經(jīng)網(wǎng)絡(luò)無(wú)法直接根據(jù)這些數(shù)字分類(lèi)，為此，我們可以考慮以下兩種方案：

單輸出：讓網(wǎng)絡(luò)輸出一個(gè)數(shù)值，若數(shù)值為正，則判斷為「葉子」；若數(shù)值為負(fù)，則判斷為「花朵」。雙輸出：讓網(wǎng)絡(luò)輸出兩個(gè)數(shù)值，第一個(gè)數(shù)值代表葉子，第二個(gè)數(shù)值代表花朵，取數(shù)值較大的那個(gè)作為分類(lèi)結(jié)果。

由于「雙輸出」的方法在后續(xù)的步驟中更通用，一般都會(huì)選擇這種方案。

以下是基于「雙輸出」的神經(jīng)網(wǎng)絡(luò)分類(lèi)結(jié)構(gòu)，讓我們逐步分析其工作原理。

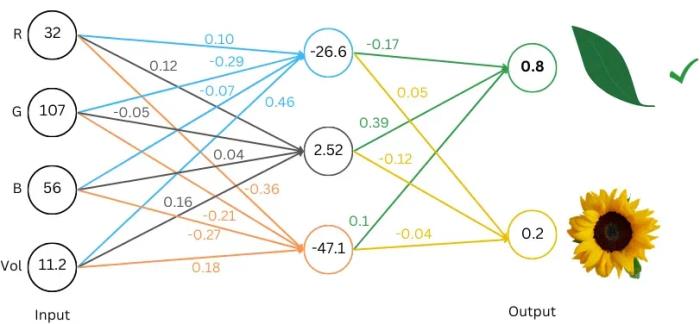
圖中圓圈內(nèi)的數(shù)值代表：神經(jīng)元 / 節(jié)點(diǎn)。連接線(xiàn)上的有色數(shù)字代表權(quán)重。每一列代表一層：神經(jīng)元的集合稱(chēng)為一層。可以將該網(wǎng)絡(luò)理解為具有三層：輸入層（4 個(gè)神經(jīng)元）、中間層（3 個(gè)神經(jīng)元）和輸出層（2 個(gè)神經(jīng)元）。

那么中間層的第一個(gè)節(jié)點(diǎn)的計(jì)算如下：

(32 * 0.10) + (107 * -0.29) + (56 * -0.07) + (11.2 * 0.46) = -26.6

要計(jì)算該網(wǎng)絡(luò)的輸出（即前向傳播過(guò)程），需要從左側(cè)的輸入層開(kāi)始。我們將已有的數(shù)據(jù)輸入到輸入層的神經(jīng)元中。接著，將圓圈內(nèi)的數(shù)字乘以對(duì)應(yīng)的權(quán)重，并將結(jié)果相加，依次傳遞到下一層。

運(yùn)行整個(gè)網(wǎng)絡(luò)后，可以看到輸出層中第一個(gè)節(jié)點(diǎn)的數(shù)值較大，表示分類(lèi)結(jié)果為「葉子」。一個(gè)訓(xùn)練良好的網(wǎng)絡(luò)可以接受不同的 (RGB, Vol) 輸入，并準(zhǔn)確地對(duì)物體進(jìn)行分類(lèi)。

模型本身并不理解「葉子」或「花朵」是什么，也不了解 RGB 的含義。它的任務(wù)僅僅是接收 4 個(gè)數(shù)字并輸出 2 個(gè)數(shù)字。我們負(fù)責(zé)提供輸入數(shù)值，并決定如何解讀輸出，例如當(dāng)?shù)谝粋€(gè)數(shù)值較大時(shí)，將其判斷為「葉子」。

此外，我們還需要選擇合適的權(quán)重，以確保模型在接收輸入后給出的兩個(gè)數(shù)值符合需求。

我們可以使用相同的網(wǎng)絡(luò)，將 (RGB, Vol) 替換為其他數(shù)值，如云量和濕度，并將輸出的兩個(gè)數(shù)值解讀為「1 小時(shí)后晴」或「1 小時(shí)后雨」。只要權(quán)重調(diào)整得當(dāng)，這個(gè)網(wǎng)絡(luò)可以同時(shí)完成分類(lèi)葉子 / 花朵和預(yù)測(cè)天氣兩項(xiàng)任務(wù)。網(wǎng)絡(luò)始終輸出兩個(gè)數(shù)字，而如何解讀這些數(shù)字 —— 無(wú)論是用于分類(lèi)、預(yù)測(cè)，還是其他用途 —— 完全取決于我們的選擇。

為了盡可能簡(jiǎn)單，剛剛的「神經(jīng)網(wǎng)絡(luò)」中省略了以下內(nèi)容：

激活層：在神經(jīng)網(wǎng)絡(luò)中，激活層的主要作用是引入非線(xiàn)性因素，使網(wǎng)絡(luò)能夠處理更復(fù)雜的問(wèn)題。如果沒(méi)有激活層，神經(jīng)網(wǎng)絡(luò)的每一層只是對(duì)輸入進(jìn)行簡(jiǎn)單的加法和乘法運(yùn)算，整體上仍然是線(xiàn)性的。即使增加多層，這樣的網(wǎng)絡(luò)也無(wú)法解決復(fù)雜的非線(xiàn)性問(wèn)題。

激活層將在每個(gè)節(jié)點(diǎn)上應(yīng)用一個(gè)非線(xiàn)性函數(shù)，常用的激活函數(shù)之一是 ReLU，其規(guī)則是：如果輸入是正數(shù)，輸出保持不變；如果輸入是負(fù)數(shù)，輸出為零。

如果沒(méi)有激活層，上一個(gè)例子中的綠色節(jié)點(diǎn)的值為 (0.10 * -0.17 + 0.12 * 0.39–0.36 * 0.1) * R + (-0.29 * -0.17–0.05 * 0.39–0.21 * 0.1) * G，所有中間層就像攤大餅一樣鋪在一起，計(jì)算也將越來(lái)越繁復(fù)。

偏置：在神經(jīng)網(wǎng)絡(luò)中，每個(gè)節(jié)點(diǎn)（也稱(chēng)為神經(jīng)元）除了接收輸入數(shù)據(jù)并進(jìn)行加權(quán)求和外，還會(huì)加上一個(gè)額外的數(shù)值，稱(chēng)為偏置。偏置的作用類(lèi)似于函數(shù)中的截距。在模型中我們又稱(chēng)它為參數(shù)。

例如，如果頂部藍(lán)色節(jié)點(diǎn)的偏置為 0.25，則節(jié)點(diǎn)的值為：(32 * 0.10) + (107 * -0.29) + (56 * -0.07) + (11.2 * 0.46) + 0.25 = -26.35。

通過(guò)引入偏置，神經(jīng)網(wǎng)絡(luò)能夠更好地?cái)M合數(shù)據(jù)，提高模型的表現(xiàn)。

Softmax：Softmax 函數(shù)用于將模型的輸出轉(zhuǎn)換為概率。它可以將任何數(shù)轉(zhuǎn)換為一個(gè)范圍在 0 到 1 之間的數(shù)，且所有元素之和為 1。這使得每個(gè)輸出值都可以轉(zhuǎn)化為對(duì)應(yīng)類(lèi)別的概率。

更多研究細(xì)節(jié)，請(qǐng)參看博客原文。

作者介紹

這篇博客的作者 Rohit Patel 在數(shù)據(jù)科學(xué)領(lǐng)域深耕了 15 年，現(xiàn)在是 Meta GenAI 數(shù)據(jù)科學(xué)總監(jiān)，參與了 Llama 系列模型的研發(fā)。

Rohit 擁有跨越多個(gè)領(lǐng)域的豐富職業(yè)經(jīng)歷。他的職業(yè)生涯始于 2002 年，在 Brainsmiths Education 擔(dān)任物理助教。隨后，他在金融領(lǐng)域從業(yè)十年。

2018 年，他加入了 Meta，擔(dān)任 Facebook Monetization 的數(shù)據(jù)科學(xué)總監(jiān)。2020 年，他創(chuàng)立了 CoFoundUp，擔(dān)任創(chuàng)始人兼首席執(zhí)行官。2021 年，他又創(chuàng)辦了 QuickAI，QuickAI 是一款專(zhuān)注于簡(jiǎn)化數(shù)據(jù)科學(xué)流程的可視化工具，用戶(hù)無(wú)需安裝任何應(yīng)用程序、插件或擴(kuò)展，即可在瀏覽器中完成數(shù)據(jù)科學(xué)任務(wù)。

參考鏈接：

https://x.com/rohanpaul_ai/status/1854226721530073162

https://towardsdatascience.com/understanding-llms-from-scratch-using-middle-school-math-e602d27ec876