新火種
2023-10-30 
深度學習蓄勢待發(fā)，即將“爆破”歐拉方程
作者｜ Jordana Cepelewicz
編譯｜錢磊、Ailleurs
編輯｜陳彩嫻250多年來，數(shù)學家們一直試圖“爆破”一些物理學中最重要的方程式，比如描述流體流動的歐拉方程。如果他們成功，他們會發(fā)現(xiàn)，在某種情況下方程會被爆破——比如可能會出現(xiàn)一個無限快地旋轉的漩渦，或者出現(xiàn)一個突然停止又突然流動的電流，或者是出現(xiàn)一個以無限快的速度掠過的電子。超過這個爆發(fā)點——也就是“奇點”——方程將不再有解。這些方程甚至將無法描述這個世界的理想情況，數(shù)學家們有理由懷疑這些流體行為的模型到底是否可靠。奇點正如其所要描述的流體一樣滑溜而不可捉摸。為了找到答案，數(shù)學家們通常會把控制流體流動的方程式輸入計算機，然后進行數(shù)字模擬。他們從一組初始條件開始，然后觀察，直到某個量的值——比如速度，或者渦度——開始瘋狂地增長，似乎在朝著爆炸的方向發(fā)展。但是計算機無法確定地發(fā)現(xiàn)奇點，原因很簡單，因為計算機無法處理無限值。如果奇點存在，計算機模型可能會接近方程被爆破的那個點，但永遠無法直接得到奇點。事實上，當用更強大的計算方法探測時，明顯的奇點卻已經(jīng)消失了。但這種對奇點的近似仍然很重要。有了近似，數(shù)學家們就可以使用一種叫做計算機輔助證明的技術來證明附近確實存在一個奇點。此前已經(jīng)有過簡化的一維版本的研究。今年早些時候，一個由數(shù)學家和地球科學家組成的團隊發(fā)現(xiàn)了一種全新的近似奇點的方法——他們利用了深度學習方法，能夠直接觀察奇點。這個團隊還用這種方法來尋找傳統(tǒng)方法無法找到的奇點，希望能證明這些方程并不像看起來那樣絕對可靠。
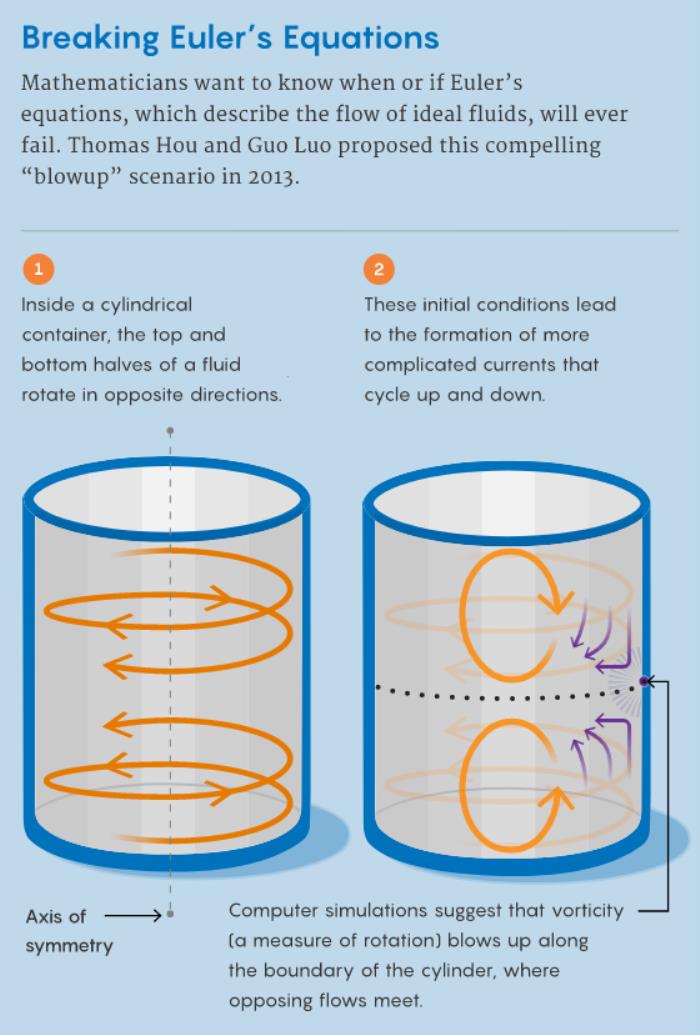
論文地址：https://arxiv.org/pdf/2201.06780v2.pdf在該研究中，Yongji Wang 等人開發(fā)了一個新的數(shù)值框架，利用基于物理信息的神經(jīng)網(wǎng)絡（physics-informed neural network，PINN）尋找Boussinesq方程的光滑自相似解。該解對應于存在圓柱邊界的三維歐拉方程的漸近自相似曲線。特別地，該解是對三維歐拉方程 Luo-Hou 爆破場景的精確描述。該解是流體力學方程的第一個真正的多維光滑向后自相似曲線。該數(shù)值框架具有魯棒性，且易于適用于其它方程。該文研究了在數(shù)學流體力學領域中具有重要意義的二維Boussinesq方程和三維帶邊界的歐拉方程的有限時間爆破問題。Yongji Wang 等人使用了一種新穎的數(shù)值方法，利用物理信息神經(jīng)網(wǎng)絡構造了Boussinesq方程的光滑向后自相似解。這個解本身可能成為未來計算機輔助證明二維Boussinesq和三維帶邊界的歐拉方程爆破的基礎。這項研究引發(fā)了一場爆破流體方程的競賽：一邊是深度學習團隊， 另一邊是多年來一直使用著更成熟的技術的數(shù)學家們。不管誰可能會贏得這場比賽——如果有人真的能夠到達終點線的話——結果都表明，神經(jīng)網(wǎng)絡可以幫助人們?yōu)樵S多不同的問題尋找新的解決方案。消失的爆破解萊昂哈德·歐拉（Leonhard Euler）在1757年提出了歐拉方程，該方程描述了理想的、不可壓縮的流體的運動——這種流體沒有粘性，也沒有內摩擦，而且不能壓縮到更小的體積。(自然界中發(fā)現(xiàn)的許多流體一樣是具有粘性的，它們的模型是納維爾-斯托克斯方程；爆破納維爾-斯托克斯方程將獲得克雷數(shù)學研究所 100萬美元的千禧年獎。) 給定流體中每個粒子在某一起始點的速度，歐拉方程應該能夠預測流體在任何時候的流動狀況。但是數(shù)學家們想知道，在某些情況下——即使一開始看起來沒什么問題——這些方程最終是否會遇到麻煩。(我們有理由懷疑這可能是事實：他們模擬的理想流體與真正的只有最輕微粘性的流體沒有任何相似之處。歐拉方程中奇點的形成可以解釋這種散度。）2013年，兩位數(shù)學家提出了這樣一個設想。由于一個完整的三維流體流動的動力學可以變得難以置信的復雜，加州理工學院的數(shù)學家Thomas Hou和香港恒生大學的Guo Luo認為流動服從某種對稱性。在他們的模擬中，流體在一個圓柱形杯內旋轉。杯子上半部分的液體順時針旋轉，而下半部分的液體逆時針旋轉。相反的水流形成了其他復雜的上下循環(huán)的水流。很快，在邊界上兩股相反的水流相遇處，流體的渦度爆發(fā)了。
PINN：始于冰川研究關于歐拉方程爆破的新研究始于這樣一個令人意想不到的領域——地球物理學家對南極洲冰蓋的動力學研究。他們的研究要求使用一種深度學習方法，這種方法后來在更多的理論背景中都被證明是有用的。數(shù)學家Tristan Buckmaster目前是普林斯頓高等研究院的訪問學者，他發(fā)現(xiàn)這種新方法純屬一次偶然。去年，他所在系的本科生Charlie Cowen Breen請他簽署一個項目，該學生在普林斯頓地球物理學家Ching-Yao Lai的指導下一直在對南極冰蓋做動力學研究。他們試圖通過衛(wèi)星圖像和其他觀測來推測冰的粘度，并預測其未來的流動。通過運用一種以前從未見過的深度學習方法——“基于物理信息的神經(jīng)網(wǎng)絡”（PINN），他們實現(xiàn)了這一點。傳統(tǒng)的神經(jīng)網(wǎng)絡需要對大量數(shù)據(jù)進行訓練才能進行預測，PINN則與此不同，它還必須滿足一組潛在的物理約束條件，包括運動定律、能量守恒、熱力學等等，以及科學家為了解決特定問題而需要引入的其他任何物理約束。
爆破解的尋求之路回顧當初，Buckmaster說，開發(fā)PINN“似乎是顯而易見要做的”。Buckmaster、Lai、Wang 以及Javier Gómez-Serrano（他是布朗大學和巴塞羅那大學的數(shù)學家）四人合作，建立了一套物理約束來幫助指導PINN，這套物理約束包括與對稱性和其他性質有關的條件，以及他們想要求解的方程。他們使用了一組使用自相似坐標來重寫的二維方程，這些方程在接近圓柱邊界的點上等價于三維歐拉方程。然后，他們訓練神經(jīng)網(wǎng)絡來尋找滿足這些約束條件的解——以及自相似參數(shù)。“這種方法非常靈活，只要施加正確的約束，你總能找到一個解。”Lai說道。事實上，團隊還通過在其他問題上測試該方法展示了這種靈活性。該團隊提供的答案看起來很像Hou 和 Luo （2013）提出的解決方案。但是數(shù)學家們希望他們給出的近似能更詳細地描述正在發(fā)生的事情，因為這是第一次直接計算出這個問題的自相似解。Sverak 表示 ：“新的研究結果更精確地說明了奇點是如何形成的”，即某些值會如何達到爆破點，以及方程將如何崩潰。Buckmaster指出：“在沒有神經(jīng)網(wǎng)絡的情況下，你很難證明你是真的在捕捉奇點的本質。很明顯，這項研究所用的方法是比傳統(tǒng)方法要容易得多。”Gómez-Serrano對此表示同意，他說：“這在未來將成為人們手邊的一種標準工具”。PINNs再一次揭示了Karniadakis所說的“隱藏流體力學”，只是這一次，他們用PINNs在更具理論性的問題上取得了進展。Karniadakis說：“我還沒見過有人用PINNs來做這件事。”這并不是數(shù)學家感到興奮的唯一原因。PINNs可能也可以用來找到另一種奇點，這種奇點用傳統(tǒng)的數(shù)值方法是幾乎發(fā)現(xiàn)不了的。這些“不穩(wěn)定”奇點可能是某些流體動力學模型中唯一存在的奇點，包括沒有圓柱邊界的歐拉方程（這一的方程求解起來已經(jīng)復雜很多）和納維-斯托克斯方程（Navier-Stokes equations）。“不穩(wěn)定的奇點確實存在。所以為什么不找到它們呢？”普林斯頓的數(shù)學家Peter Constantin曾這樣說道。但即使對于用經(jīng)典方法可以處理的穩(wěn)定奇點，PINN為有圓柱邊界的歐拉方程提供的解決方案“是定量且精確的，并且還可以變得更為嚴密。現(xiàn)在有了一個通往證明的路線圖。這將需要做很多工作，需要很多的技能。我想這還需要一些創(chuàng)意。但我不認為這需要什么天賦。我認為這是可行的。”Fefferman這樣表示。Buckmaster的團隊現(xiàn)在正在與Hou和Chen展開一項競賽，看誰能搶先到達終點線。Hou和Chen在 這條賽道上是領先一步的：據(jù)Hou說，他們在過去幾年里在改進近似解和完成證明方面取得了實質性進展，他懷疑Buckmaster和他的同事必須改進近似解，才能得到他們自己的證明。而他認為，現(xiàn)有近似解的誤差余地已經(jīng)很小了。盡管如此，許多專家希望，250年來人們對歐拉方程爆破解的探索將接近尾聲。Sverak 說：“從概念上講，我認為……所有重要的部分都已到位，只是細節(jié)還很難確定。”
參考鏈接：
https://www.quantamagazine.org/deep-learning-poised-to-blow-up-famed-fluid-equations-20220412/
https://arxiv.org/pdf/2201.06780v2.pdf
相關推薦
- 免責聲明
- 本文所包含的觀點僅代表作者個人看法，不代表新火種的觀點。在新火種上獲取的所有信息均不應被視為投資建議。新火種對本文可能提及或鏈接的任何項目不表示認可。 交易和投資涉及高風險，讀者在采取與本文內容相關的任何行動之前，請務必進行充分的盡職調查。最終的決策應該基于您自己的獨立判斷。新火種不對因依賴本文觀點而產(chǎn)生的任何金錢損失負任何責任。
