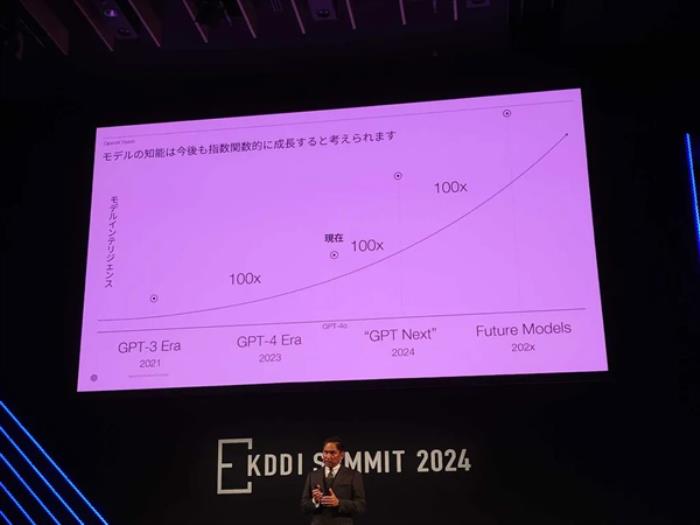
o1方法性能無上限!姚班馬騰宇等數學證明:推理token夠多,就能解決任意問題
OpenAI用o1開啟推理算力Scaling Law,能走多遠?
數學證明來了:沒有上限。
斯隆獎得主馬騰宇以及Google Brain推理團隊創建者Denny Zhou聯手證明,只要思維鏈足夠長,Transformer就可以解決任何問題!

通過數學方法,他們證明了Transformer有能力模擬任意多項式大小的數字電路,論文已入選ICLR 2024。

用網友的話來說,CoT的集成縮小了Transformer與圖靈機之間的差距,為Transformer實現圖靈完備提供了可能。

這意味著,神經網絡理論上可以高效解決復雜問題。
再說得直白些的話:Compute is all you need!
首先需要說明的是,“可以解決任何問題”是一個通俗化的表述,嚴格來說,論文的核心結論是思維鏈(CoT)能夠顯著提升Transformer的表達能力。
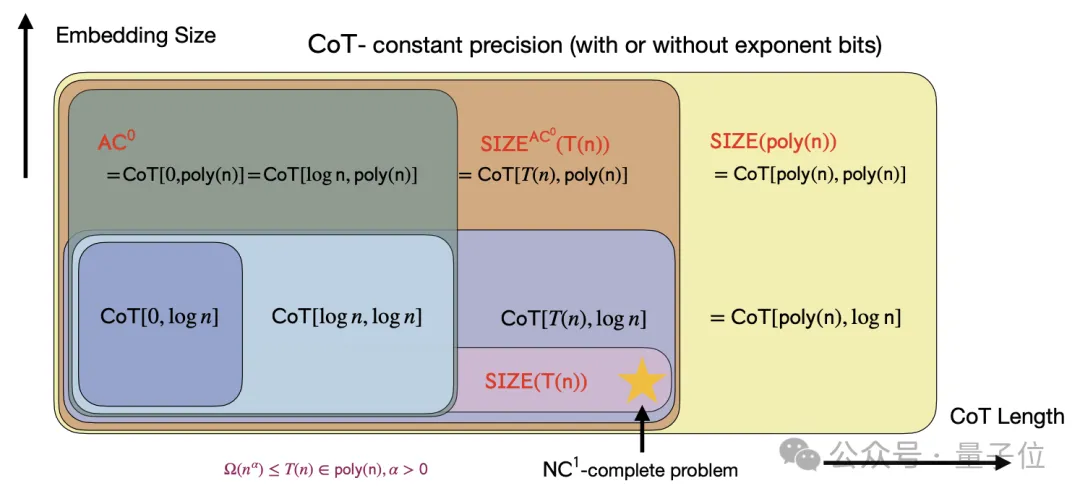
作者首先通過理論分析,提出對于固定深度、多項式寬度、常數精度的Transformer模型,如果不使用CoT,其表達能力將受限于AC0問題類別。(AC0是一類可以在并行計算中高效解決的問題,但不包括需要復雜序列化計算的問題。)
在固定指數位的情況下,固定深度、對數精度的Transformer模型即使引入了正確的舍入操作,其表達能力也僅限于TC0問題類別。
但當引入CoT時,固定深度、常數精度的Transformer模型就能夠解決任何由大小為T的布爾電路解決的問題。
這表明CoT顯著擴展了模型的表達能力,使其能夠處理更復雜的問題。
為了驗證理論分析,論文在四個核心問題上進行了實驗,考慮了基礎(base)、CoT和提示(hint)三種不同的訓練設置:
模運算(Modular Addition):并行計算問題,論文展示了CoT如何提高模型在這個問題上的準確性;置換群組合(Permutation Composition):需要序列化計算的問題,論文證明了CoT在解決這類問題上的有效性;迭代平方(Iterated Squaring):典型的序列化計算問題,論文展示了CoT如何使模型能夠有效地解決這類問題;電路值問題(Circuit Value Problem):這是一個P完全問題,論文證明了即使是在模型深度較低的情況下,CoT也能使模型能夠解決這類問題。首先在可并行的模運算問題上,輸入是若干個模7的數,輸出是它們的模7和。
實驗結果表明,所有設置下的Transformer都能夠學習模加;但在較長序列(如n=16)上,CoT的優勢更加明顯。
這說明即使是可并行問題,CoT也能帶來一定的效率提升。
在內在串行的置換群復合任務上,輸入是S_5置換群中的若干個置換,輸出是它們的復合結果。
結果,CoT提高了低深度模型的準確性——
不使用CoT的Transformer即使深度較大也難以學習該任務(準確率約20%),而使用CoT后即使是1層Transformer也能輕松學習(準確率100%)。
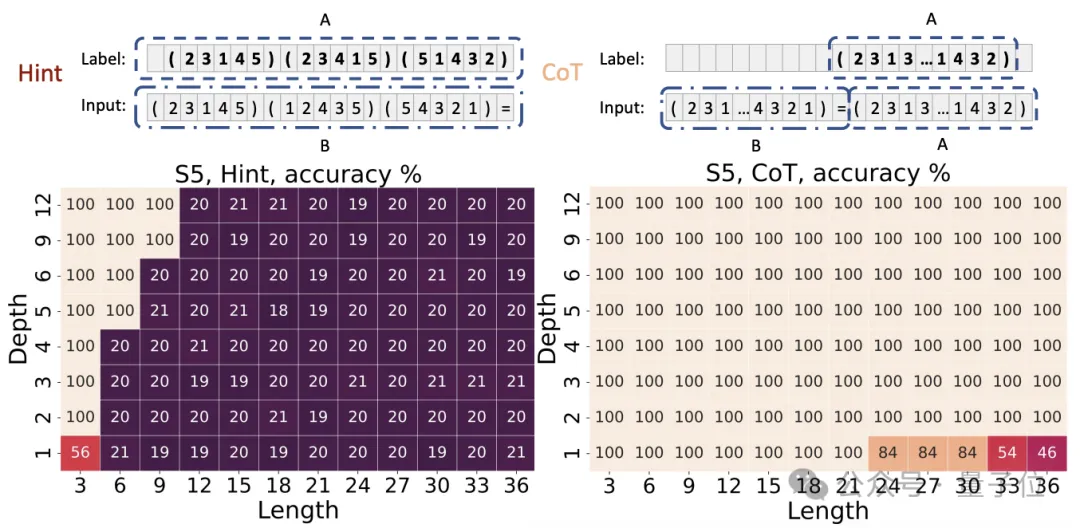
對于迭代平方任務,輸入是一個質數p、一個整數r和若干個“^2”符號,輸出是r^(2^k) mod p。
實驗結果與置換群復合任務相似:不使用CoT時。即使16層Transformer也難以學習;而使用CoT后。1層Transformer就能完美求解。
這再次驗證了理論分析,即迭代平方是內在串行的,需要CoT來提供必要的計算能力。
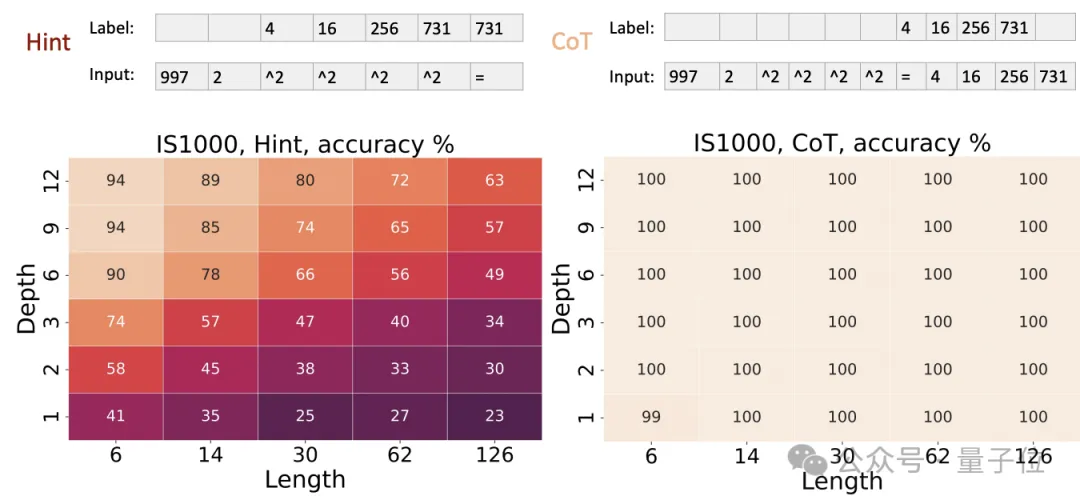
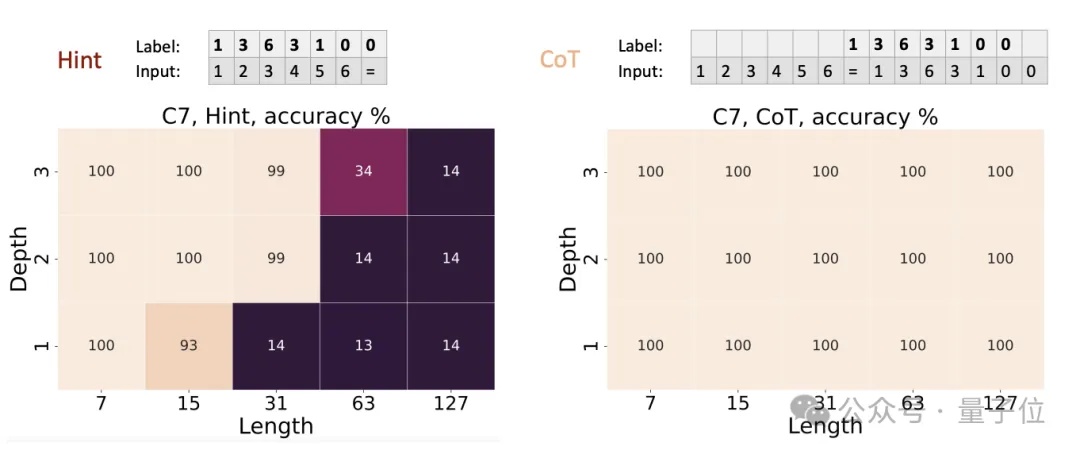
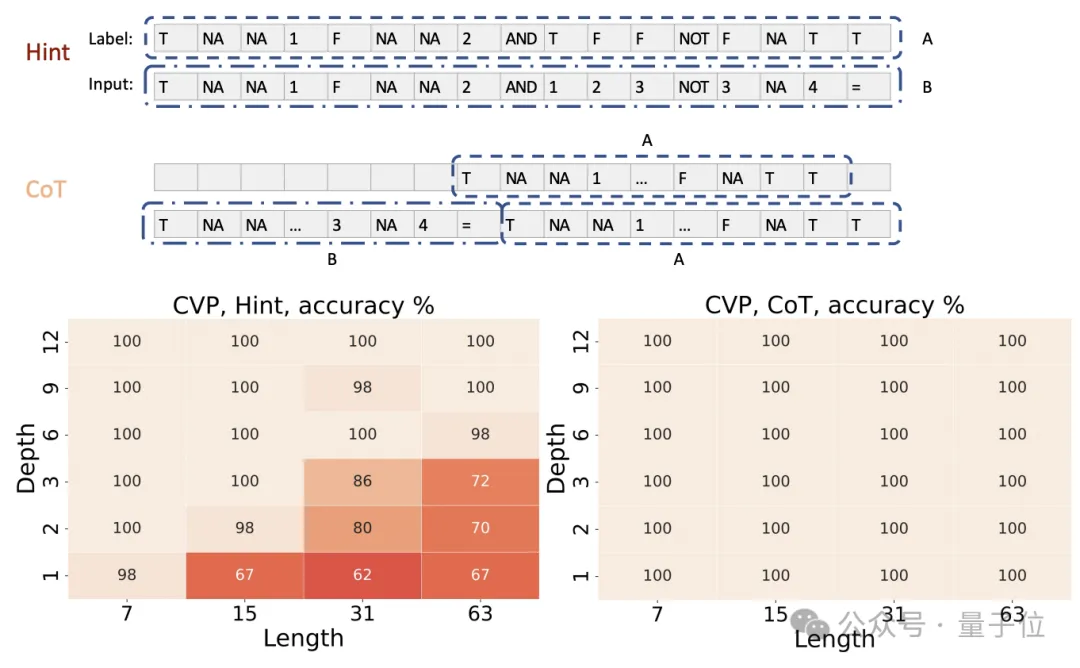
最后的電路值問題,輸入是一個隨機布爾電路的描述,輸出是電路的最終輸出值。
實驗結果表明,在基準設置下,4層Transformer的準確率約為50%,8層約為90%,16層接近100%;
而使用CoT后,1層Transformer就能達到接近100%的準確率。
這驗證了理論結果,即CoT賦予了Transformer任意電路的模擬能力,使其能夠解決電路值問題這一P完全問題。
除了上述實驗,作者還對以下結論進行了理論證明:
證明的思路是先將布爾電路視為一系列邏輯門的組合,然后利用Transformer中的位置編碼為每個邏輯門及其狀態分配一個獨特的表示,進而通過逐步計算來模擬整個電路的執行過程。
這個證明的關鍵,在于利用CoT來逐步模擬電路中每個門的計算。
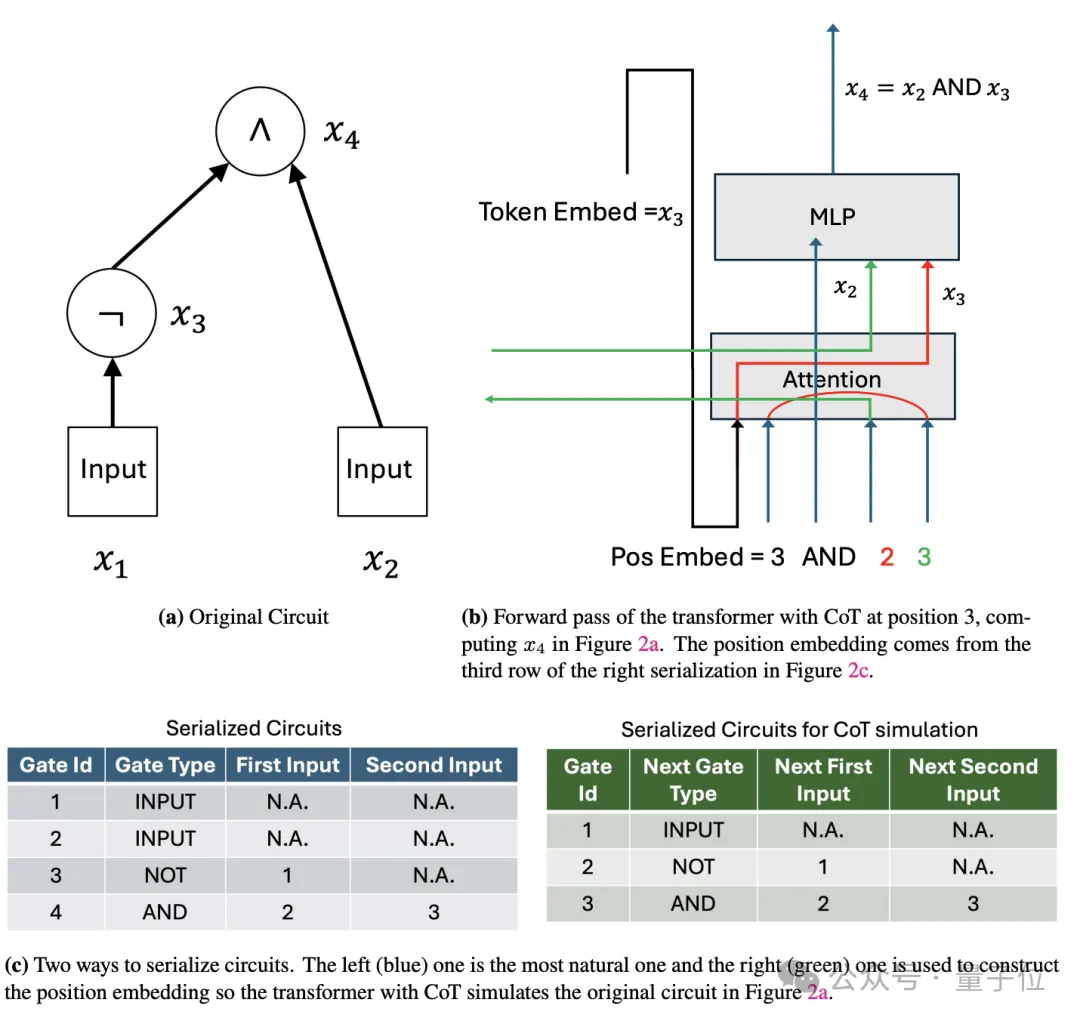
具體而言,對于一個有T(n)個門的電路,作者設計了一個4T(n)個token的輸入序列。
這個序列包含了電路的完整描述,每個門用4個連續的token表示:門類型、兩個輸入門的索引和當前門的索引,并用輸入序列中的第一個token指示了電路的輸入值。
然后,作者構造了一個常數深度的Transformer,這個Transformer的嵌入維度只需要O(log n),就足以對T(n)個門進行編碼。
在第一層,Transformer讀取輸入序列,并將電路的描述信息存儲到其位置嵌入中。
接下來是關鍵的CoT步驟。Transformer逐步生成4T(n)個token的思維鏈,每4個token對應電路中的一個門。
對于第i個門,Transformer執行以下操作:
利用注意力機制獲取兩個輸入門的計算結果:如果輸入門是電路的輸入,可以直接從輸入序列中讀取;如果輸入門是前面計算過的中間結果,則可以從思維鏈的對應位置讀取。根據門的類型(與、或、非等),用前饋網絡計算當前門的輸出。將當前門的輸出寫回到思維鏈中,作為后續門的輸入。通過這一過程,Transformer逐步模擬了電路中每一個門的計算,并將中間結果存儲在思維鏈中。在生成完整個思維鏈后,最后一個門的輸出就對應了電路的最終輸出。
也就是說,通過將電路“展開”為一個長度為O(T(n))的思維鏈,即使固有深度很淺,Transformer也可以逐步執行電路中的計算。
在此基礎上,作者進一步證明,具有O(T(n))長度CoT的常數深度Transformer,可以模擬任意T(n)大小的電路,因此其計算能力等價于多項式大小電路。
理論打通了,實際可行嗎?能夠模擬電路的計算過程,意味著CoT+Transformer能夠解決可計算問題。
同時,這也說明只要有足夠的CoT思考時間,大模型不需要擴展尺寸也能解決復雜問題。
有專業人士用一篇長文解釋了CoT和圖靈完備性之間的關系:

還有人把這項成果和OpenAI的“草莓”,也就是爆火的超強模型o1聯系到了一起——
草莓同樣也是思考的時間越長,準確性越高,按照這個思路,只要有好的模型,就能解決人類面臨的一系列難題。
甚至有人表示,如果這項研究是真的,那么AGI就已經在到來的路上了……

不過也有人認為,這只是一個理論性的結果,距離實際應用還存在很大差距。
即使拋開理論與實際條件的不同,時間和成本問題就是一個重要的限制因素。
而且實驗的一個假設是模型權重被正確設置,但實際模型的訓練很難達到這一程度。

還有人指出,這種模擬門電路運算,并不是大模型實際學習和工作的方式。

換言之,如何將實際問題用布爾電路表示,是Transformer從能解決運算問題到能夠解決實際問題的一個關鍵。
但現實中,諸如“如何治療癌癥”這樣的問題,很難以電路的形式去描述。
雖然距離實際應用還有一系列問題要解決,但這項研究至少揭開了CoT的巨大潛力。
作者簡介本論文一共有四名作者,全部都是華人。
按署名順序,第一位作者為清華姚班校友李志遠,是馬騰宇已畢業的博士生,現為芝加哥豐田技術學院(TTIC)的終身教授助理教授。
第二位作者是Hong Liu,也是馬騰宇的博士生,現在在讀,本科就讀于清華,曾獲得特等獎學金及優秀畢業生榮譽。
第三位是Google Brain推理團隊創建者Denny Zhou,中科院博士,2017年加入Google前在微軟擔任了11年的高級研究員。
最后是2021年斯隆獎得主、斯坦福大學助理教授馬騰宇,他是姚班校友、陳丹琦的同班同學。
論文地址:https://arxiv.org/abs/2402.12875參考鏈接:[1]https://x.com/denny_zhou/status/1835761801453306089[2]https://www.reddit.com/r/singularity/comments/1fiemv4/denny_zhou_founded_lead_reasoning_team_at_google/
- 免責聲明
- 本文所包含的觀點僅代表作者個人看法,不代表新火種的觀點。在新火種上獲取的所有信息均不應被視為投資建議。新火種對本文可能提及或鏈接的任何項目不表示認可。 交易和投資涉及高風險,讀者在采取與本文內容相關的任何行動之前,請務必進行充分的盡職調查。最終的決策應該基于您自己的獨立判斷。新火種不對因依賴本文觀點而產生的任何金錢損失負任何責任。





 新火種
2024-09-18
新火種
2024-09-18