九九热视频精品在线_国产成人mv视频在线观看_国产精品三级一区二区_亚洲精品国产av成拍色拍婷婷_久久伊人一区二区_国产高清精品网站_九九99热久久精品离线6_国产在线一卡2卡三卡4卡免费_日韩美女乱淫aaa高清视频_亚洲大胆_啪啪一级视频_午夜av免费观看_国产高清精品福利私拍国产写真_亚洲婷婷五月综合狠狠_日韩欧美一区二区三区视频_岛国av免费看_精品国产乱码久久久久久久软件_亚洲国产成人精品无码区99_www日本色_免费黄色看片

該論文的第一作者是山東大學碩士二年級學生徐瑞，指導教師是山東大學交叉研究中心的屠長河教授和辛士慶副教授。合作者還包括香港大學的博士生竇志揚、美國德州大學達拉斯分校的博士生王寧娜、青島科技大學的陳雙敏副教授、山東大學的江銘炎教授、美國德州大學達拉斯分校的郭小虎教授以及美國德州農工大學的王文平教授。

論文項目主頁：https://xrvitd.github.io/Projects/GCNO/index.html

代碼：https://github.com/Xrvitd/GCNO

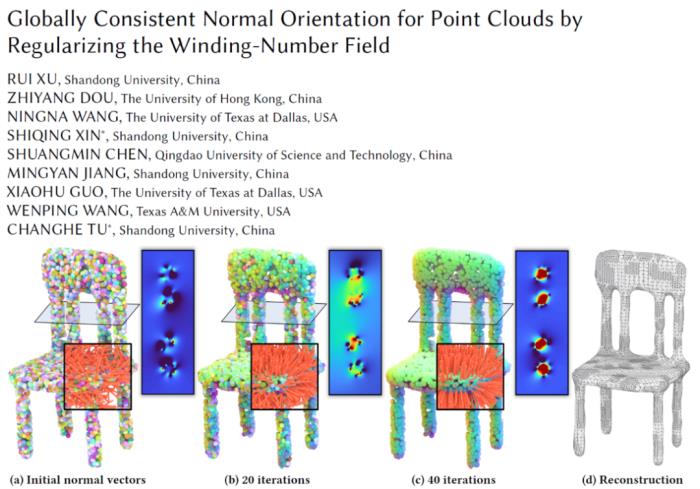
論文的研究主題是點云法線定向問題。考慮到傳統方法未能充分利用形狀全局先驗（流形、水密、可定向），作者利用全局一致法向與規范卷繞數場（Winding Number Field）之間的強耦合關系，提出了一個光滑的優化函數，從而獲取能夠反映潛在形狀的定向信息。
點云數據可以認為是一組落在某個可定向水密流形曲面上的采樣點集。估算法向是三維重建任務的重要一步，并為很多幾何處理任務提供必要的信息支持。具體地說，法向的估算又可細分為定向一致性問題和法向精確性問題。然而，原始點云可能存在各種瑕疵（噪聲、稀疏、不均勻、缺失等），潛在形狀可能非常復雜（薄板、細管、尖邊尖角、高虧格），這進一步加劇了法向估算的難度。本論文觀察到定向一致性問題和法向精確性問題不是兩個獨立的問題，因此將它們一并考慮，針對無法向點云直接恢復具有精確性和一致性的法向信息。
傳統定向算法多是基于傳播的范式，由近及遠，層層向外傳播。然而，這種過程式的算法存在 “一步錯，步步錯” 的先天缺陷。歸根到底，如何充分利用形狀全局先驗，以克服點云數據存在的二義性，是解決該困難問題的關鍵。作者觀察到正確的定向能夠產生規范的卷繞數場（非 0 即 1），因而以 “編碼了全局形狀信息的卷繞數場” 為工具，提出了基于規范化卷繞數場的新思路。如圖 1 所示，當點云的法線完全隨機時，點云的卷繞數場幾乎處處為零；而當點云的法線完全正確時，點云的卷繞數場非 0 即 1，且模型外部為 0，內部為 1。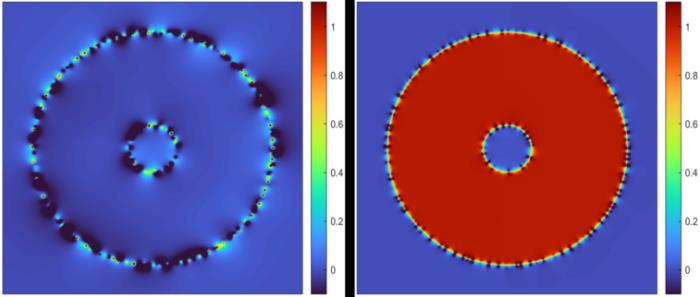

圖 1. 左側為隨機法向產生的卷繞數場，右側為正確法向產生的卷繞數場如圖 2 所示，為了迫使卷繞數 “非 0 即 1”，作者使用物理學中的雙勢阱函數鼓勵卷繞數向 0 或者 1 演化。同時，為了阻止全零卷繞數，本文在雙勢阱函數中添加了一個修正項，進一步提高取值為 1 的傾向性。其對應的函數是：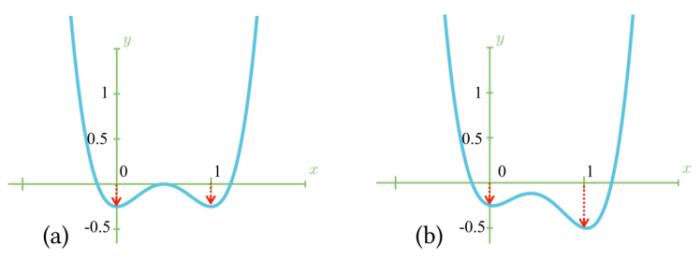

圖 2. 普通雙勢阱函數及修正后的函數圖像作者觀察到，盡管定向一致性問題和法向精確性問題分別反映了全局和局部幾何結構，但它們之間存在關聯。已有研究表明，空間 Voronoi 圖能夠描述局部幾何結構，在法線準確估計方面具備優勢。因此，本文首先求解三維空間中的 Voronoi 圖，然后以 Voronoi 頂點作為觀測點，定義法向的全局一致性和局部精確性。假設共有 M 個 Voronoi 頂點，那么卷繞數場的規范性可被描述為：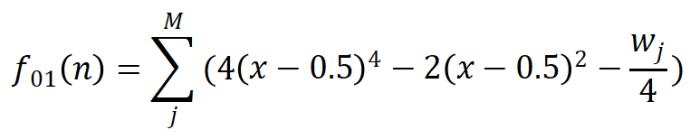



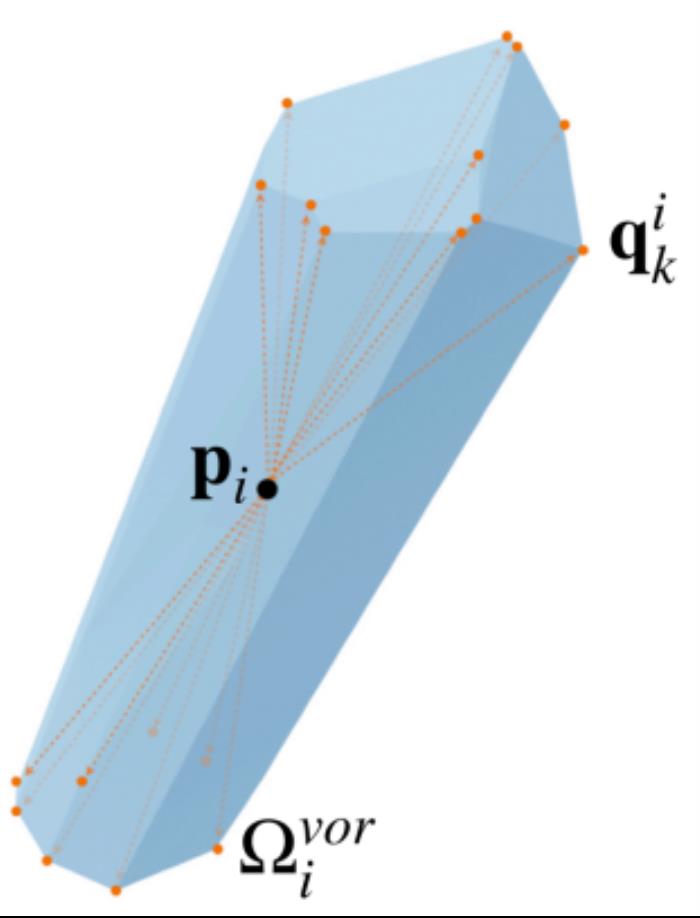
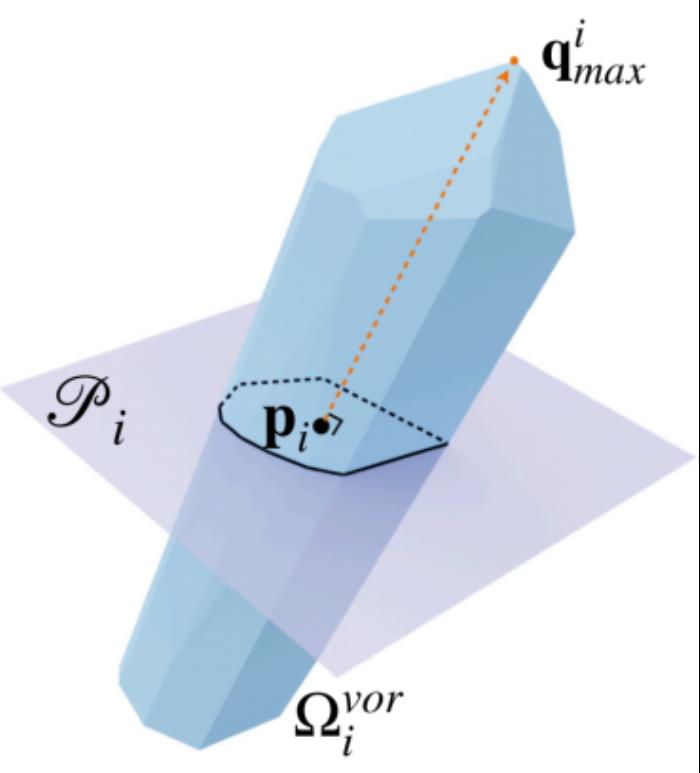
圖 3. 每個點的 Voronoi cell，上圖為 Voronoi 頂點，下圖為極點 (最遠點)在采樣比較稠密的情況下，每個采樣點的 Voronoi cell 部分在內、部分在外。外部 Voronoi 頂點對應的卷繞數為 0，內部 Voronoi 頂點對應的卷繞數為 1。為了抑制 “全 0” 或者 “全 1” 的情況，確保潛在曲面將三維空間分為內外兩部分，引入平衡項：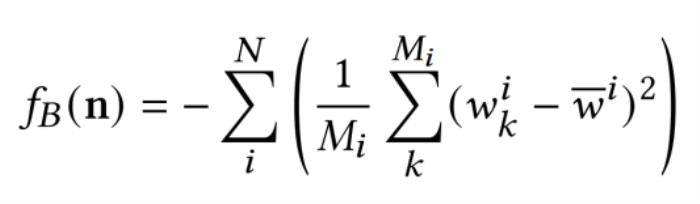

如圖 3 所示，對于 Voronoi cell 來說，有一個離站點最遠的內部頂點和一個離站點最遠的外部頂點，它們均稱作極點。已有研究表明，極點為法線朝向的精確性提供了幾何依據。因此，論文還引入一個對齊項，用于刻畫法線的走向是否與極點所處的方位保持一致：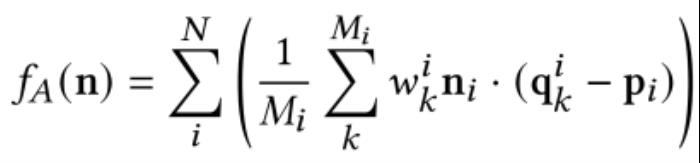


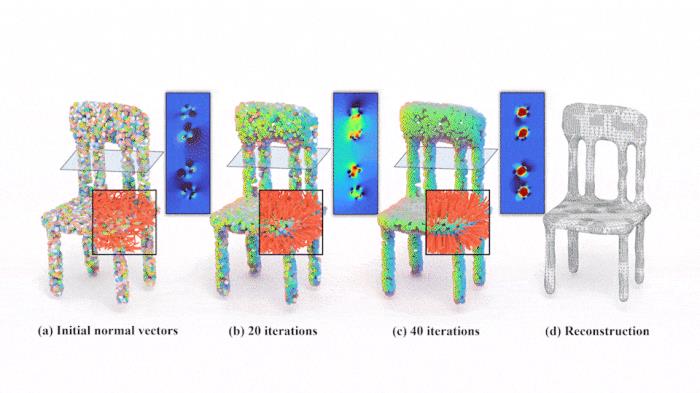
圖 4. 迭代優化過程最終，一致性需求和精確性需求被描述為一個由三個能量項構成的目標函數，其最小值反映了一致性和精確性：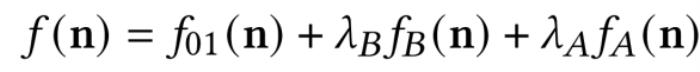

其中 n 為點云的待求法向。作者嚴格地證明了該目標函數存在非平凡的最優解。優化過程如圖 4 所示。即使對于薄板、細管等具有挑戰性的模型，無論是隨機法線初始化還是球面法線初始化，均能得到整齊的法線信息。

圖 5. 法向一致性結果對比 (紅色點為預測錯誤)
圖 6. 稀疏點云泊松重建結果本文對現有的法線估計算法進行了比較（圖 5），并使用泊松重建（Poisson Reconstruction）進行了黑盒測試（圖 6），充分表明了該方法的有效性。即使在稀疏、噪聲、復雜（圖 7）甚至只有線框（圖 8）的模型上，該算法仍能獲得高質量的法線信息和重建結果。

圖 7. 復雜模型重建結果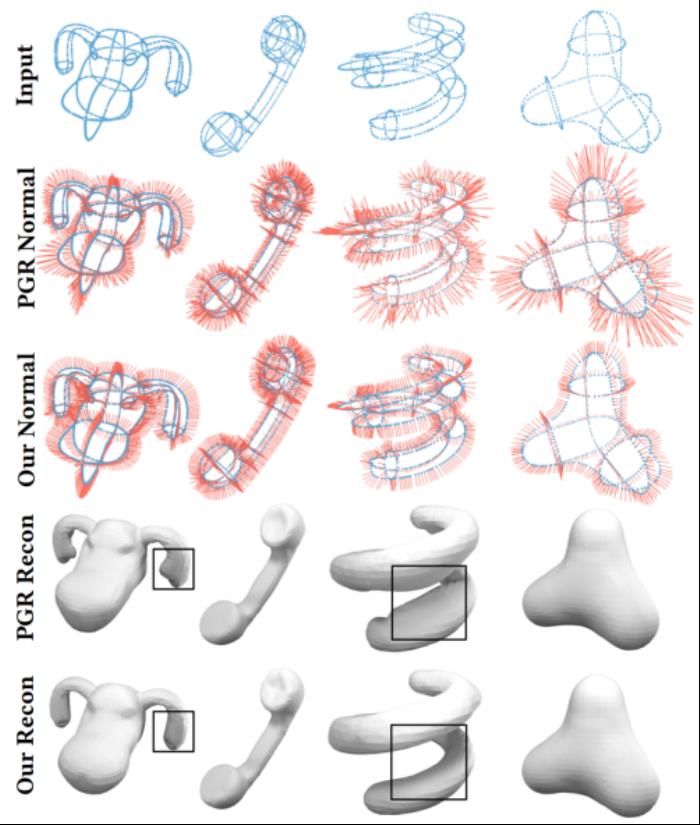
圖 8. 線框點云法向估計及重建結果總結起來，本文提出了一種通過規范化卷繞場獲得全局一致法線的方法。該方法以卷繞數場非 0 即 1 為基本要求，同時考慮了精確性（與 Voronoi 極點對齊）和內外可分性（0-1 平衡），將法線定向問題轉化為一個最小化問題。本文對具有各種缺陷和挑戰的點云進行了廣泛實驗，例如噪聲、稀疏、縫隙、薄板和高度復雜的幾何 / 拓撲結構，實驗結果表明了該方法的優越性。該技術有望應用于逆向工程、智能制造、三維影像、無人駕駛、人機交互、數字城市、電影娛樂等領域。值得一提的是，論文相關視頻還入選了 SIGGRAPH 2023 技術論文宣傳片，突顯了其重要性和創新性。

山東大學交叉研究中心（Interdisciplinary Research Center, IRC）成立于 2013 年 9 月，重點關注視覺感知與交互相關領域新興技術的發展與應用。自成立以來，中心面向國家在智能制造、虛擬現實與增強現實、大數據可視化、智能機器人等方面的重大需求，建設計算機圖形學、計算機視覺、可視化與可視分析三個方向。