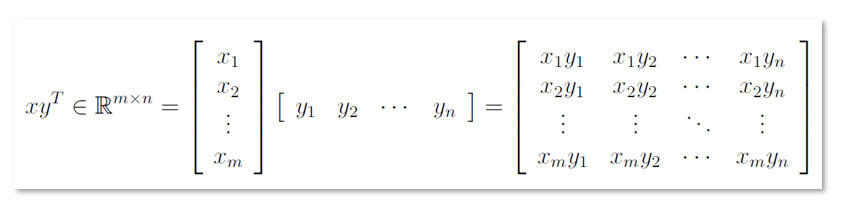深度學習和機器學習的線性代數入門
本文目錄
引言
機器學習ML和深度學習NN中的線性代數
矩陣
向量
矩陣乘法
轉置矩陣
逆矩陣
正交矩陣
對角矩陣
正規方程的轉置矩陣和逆矩陣
線性方程
向量范數
L1范數/Manhattan范數
L2范數/Euclidean范數
ML中的正則化
Lasso
嶺
特征選擇與抽取
協方差矩陣
特征值與特征向量
正交性
正交集
擴張空間
基
主成分分析(PCA)
矩陣分解
總結
引言
機器學習和深度學習建立在數學原理和概念之上,因此AI學習者需要了解基本數學原理。在模型構建過程中,我們經常設計各種概念,例如維數災難、正則化、二進制、多分類、有序回歸等。
神經元是深度學習的基本單位,該結構完全基于數學概念,即輸入和權重的乘積和。至于Sigmoid,ReLU等等激活函數也依賴于數學原理。
正確理解機器學習和深度學習的概念,掌握以下這些數學領域至關重要:
線性代數
微積分
矩陣分解
概率論
解析幾何
機器學習和深度學習中的線性代數
在機器學習中,很多情況下需要向量化處理,為此,掌握線性代數的知識至關重要。對于機器學習中典型的分類或回歸問題,通過最小化實際值與預測值差異進行處理,該過程就用到線性代數。通過線性代數可以處理大量數據,可以這么說,“線性代數是數據科學的基本數學。”
在機器學習和深度學習中,我們涉及到線性代數的這些知識:
向量與矩陣
線性方程組
向量空間
偏差
通過線性代數,我們可以實現以下機器學習或深度學習方法:
推導回歸方程
通過線性方程預測目標值
支持向量機SVM
降維
均方差或損失函數
正則化
協方差矩陣
卷積
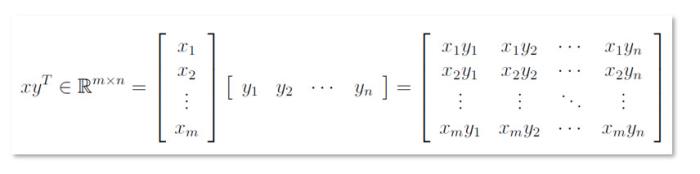
矢量積
矩陣
矩陣是線性代數的重要概念。一個m*n矩陣包含mn個元素,可用于線性方程組或線性映射的計算,也可將其視為一個由m*n個實值元素組成的元組。
矩陣表示
向量
在線性代數中,向量是大小為n*1的矩陣,即只有一列。
矩陣表示
矩陣乘法
矩陣乘法是行和列的點積,其中一個矩陣的行與另一個矩陣列相乘并求和。
矩陣乘法
矩陣乘法在線性回歸中的應用
通過多種特征可以預測房屋價格。下表展示了不同房屋的特征及其價格。
不同房屋的特征及其價格
特征變量與目標變量
令:
特征及其系數
房價預測函數
轉置矩陣
對于矩陣A∈R^m*n,有矩陣B∈R^n*m滿足b_ij = a_ij,稱為A的轉置,即B=A^T。
A的轉置
逆矩陣
對n階矩陣A,有矩陣B∈R^n*n滿足AB =I_n(單位矩陣)= BA的性質,稱B為A的逆,表示為A^-1。
矩陣A和B
A和B相乘
A、B互為逆矩陣(得到單位矩陣)
正交矩陣
當且僅當矩陣列向量組是單位正交向量組時,n階矩陣A∈R^n*n是正交矩陣,有:
正交矩陣
矩陣A及其轉置
矩陣A及其轉置的乘積
對角矩陣
在n階矩陣A∈R^n*n中,除主對角線上的元素,其他所有元素均為零,稱其為對角矩陣,即:
Aij =0,i != j
對角矩陣
正規方程的轉置矩陣和逆矩陣
正規方程通過計算theta j的導數,將其設為零來最小化J。無需Gradient Descent就可直接得到θ的值,θ見下圖。
最小化誤差
通過上式實現前文“房價預測”。
以矩陣形式表示特征x和目標值y
創建特征x和目標y的矩陣:
import numpy as np Features
x = np.array([[2, 1834, 1],[3, 1534, 2],[2, 962, 3]])# Target or Pricey = [8500, 9600, 258800]
計算x的轉置:
# Transpose of xtranspose_x = x.transpose()transpose_x
特征x矩陣的轉置
轉置矩陣與原矩陣x的乘積:
multi_transpose_x_to_x = np.dot(transpose_x, x)
轉置矩陣與原矩陣x的乘積
轉置矩陣與原始矩陣乘積的逆:
inverse_of_multi_transpose_x_to_x = np.linalg.inv(multi_transpose_x_to_x)
逆矩陣
x的轉置與y的乘積:
multiplication_transposed_x_y = np.dot(transpose_x, y)
x的轉置與y的乘積
theta值計算:
theta = np.dot(inverse_of_multi_transpose_x_to_x, multiplication_transposed_x_y)
theta
線性方程
線性方程是線性代數的核心,通過它可以解決許多問題,下圖是一條直線方程。
線性方程y=4x-5及其圖示
當x=2時:
由上述線性方程式得出的y
線性回歸中的線性方程
回歸就是給出線性方程的過程,該過程試圖找到滿足特定數據集的最優曲線,即:
Y = bX + a
其中,a是Y軸截距,決定直線與Y軸相交的點;b是斜率,決定直線傾斜的方向和程度。
示例
通過線性回歸預測平方英尺和房屋價格的關系。
數據讀取:
import pandas as pd
df = pd.read_csv('house_price.csv')
df.head()
房價表
計算均值:
def get_mean(value):
total = sum(value)
length = len(value)
mean = total/length
return mean
計算方差:
def get_variance(value):
mean = get_mean(value)
mean_difference_square = [pow((item - mean), 2) for item in value]
variance = sum(mean_difference_square)/float(len(value)-1)
return variance
計算協方差:
def get_covariance(value1, value2):
value1_mean = get_mean(value1)
value2_mean = get_mean(value2)
values_size = len(value1)
covariance = 0.0 for i in range(0, values_size):
covariance += (value1[i] - value1_mean) * (value2[i] - value2_mean)
return covariance / float(values_size - 1)
線性回歸過程:
def linear_regression(df):
X = df['square_feet']
Y = df['price']
m = len(X)
square_feet_mean = get_mean(X)
price_mean = get_mean(Y)
#variance of X
square_feet_variance = get_variance(X)
price_variance = get_variance(Y)
covariance_of_price_and_square_feet = get_covariance(X, Y)
w1 = covariance_of_price_and_square_feet / float(square_feet_variance) w0 = price_mean - w1 * square_feet_mean
# prediction --> Linear Equation
prediction = w0 + w1 * X
df['price (prediction)'] = prediction
return df['price (prediction)']
以上級線性回歸方法:
linear_regression(df)
預測價格
線性回歸中的線性方程:
向量范數
向量范數可用于衡量向量的大小,也就是說,范數|| x ||表示變量x的大小,范數|| x-y ||表示兩個向量x和y之間的距離。
向量范數計算公式:
常用的向量范數為一階和二階:
一階范數也叫Manhattan范數
二階范數也叫Euclidean范數
在正則化中會用到一階和二階范數。
一階范數/Manhattan范數
x∈R^n的L1范數定義為:
一階范數示意圖
L2范數/Euclidean范數
x∈R^n的L2范數定義為:
二階范數示意圖
機器學習中的正則化
正則化是指通過修改損失函數以懲罰學習權重的過程,是避免過擬合的有效方式。
正則化在機器學習中的作用:
解決共線性問題
除去噪聲數據
避免過擬合
提升模型表現
標準正則化技術包括:
L1正則化(Lasso)
L2正則化(Ridge)
L1正則化(Lasso)
Lasso正則化應用廣泛,其形式為:
L2正則化(Ridge)
Ridge正則化表達式:
其中,通過λ調整懲罰項的權重進行控制。
特征提取和特征選擇
特征提取和特征選擇的主要目的是選擇一組最佳的低維特征以提高分類效率,以避免維數災難。在實踐中,通過矩陣操作實現特征選擇和特征提取。
特征提取
在特征提取中,我們通過映射函數從現有特征中找到一組新特征,即:
特征選擇
特征選擇是指從原始特征中選擇部分特征。
主要特征抽取方法包括主成分分析PCA和線性判別分析LDA。其中,PCA是一種典型的特征提取方法,了解協方差矩、特征值或特征向量對于理解PCA至關重要。
協方差矩陣
在PCA推導過程中,協方差矩陣起到至關重要的作用。以下兩個概念是計算協方差矩陣的基礎:
方差
協方差
方差
方差的局限性在于,無法表示變量之間的關系。
協方差
協方差用于衡量兩個變量之間的關系:
協方差矩陣
協方差矩陣是方陣,其中每個元素表示兩個隨機矢量之間的協方差。
協方差矩陣的計算公式:
特征值與特征向量
特征值:令m為n*n矩陣,如果存在非零向量x∈R^n,使得mx =λx,則標量λ為矩陣m的特征值。
特征向量:上式中向量x稱為特征值λ的特征向量。
特征值與特征向量的計算
若n階矩陣m有特征值λ和相應特征向量x,有mx =λx,則mx —λx= 0,得到下式:
求解方程的λ可得到m的所有特征值
示例:
計算一下矩陣的特征值和特征向量。
解:
因此,矩陣m有兩個特征值2和-1。每個特征值對應多個特征向量。
正交性
如果向量v和w的點積為零,稱兩向量正交。
v.w = 0
例如:
正交集
如果某一集合中的所有向量相互正交,且均為單位長度,稱為規范正交集合。其張成的子空間稱為規范正交集。
擴張空間
令V為向量空間,元素v1,v2,…..,vn∈V。
將這些元素與標量相乘加和,所有的線性組合集稱為擴張空間。
示例:
Span (v1, v2, v3) = av1 + bv2 + cv3
基
向量空間的基是一組向量,通過基向量的線性可以組成向量空間中任意一個元素。
示例:
假設向量空間的一組基為:
基向量元素是相互獨立的,如:
主成分分析PCA
通過PCA能夠對數據進行降維,以處理盡可能多的數據。其原理是:找到方差最大的方向,在該方向上進行投影以減小數據維度。
PCA的計算方法:
設有一個N*1向量,其值為x1,x2,…..,xm。
1.計算樣本均值
2.向量元素減均值
3.計算樣本協方差矩陣
4.計算協方差矩陣的特征值和特征向量
5.降維:選擇前k個特征向量近似x(k
python實現主成分分析
為實現PCA,需要實現以下功能:
獲取協方差矩陣
計算特征值和特征向量
通過PCA了解降維
Iris數據導入
import numpy as np
import pylab as pl
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as pltfrom sklearn.preprocessing import StandardScaler load_iris = datasets.load_iris() iris_df = pd.DataFrame(load_iris.data, columns=[load_iris.feature_names]) iris_df.head()
標準化
標準化數據使得所有特征數據處于同一量級區間,有利于分析特征。
standardized_x = StandardScaler().fit_transform(load_iris.data)
standardized_x[:2]
計算協方差矩陣
covariance_matrix_x = np.cov(standardized_x.T)
covariance_matrix_x
計算協方差矩陣得特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix_x)
eigenvalues
eigenvectors
特征值的方差
total_of_eigenvalues = sum(eigenvalues)
varariance = [(i / total_of_eigenvalues)*100 for i in sorted(eigenvalues, reverse=True)]
varariance
上圖中的方差值分別表示:
1st 成分 = 72.96%
2nd 成分 = 22.85%
3rd 成分 = 3.5%
4th 成分 = 0.5%
可以看到,第三和第四成分具有很小的方差,可以忽略不記,這些組分不會對最終結果產生太大影響。
保留占比大的第一、第二成分,并進行以下操作:
eigenpairs = [(np.abs(eigenvalues[i]), eigenvectors[:,i]) for i in range(len(eigenvalues))]
# Sorting from Higher values to lower valueeigenpairs.sort(key=lambda x: x[0], reverse=True) eigenpairs
計算Eigenparis的矩陣權重
matrix_weighing = np.hstack((eigenpairs[0][1].reshape(4,1),eigenpairs[1][1].reshape(4,1)))
matrix_weighing
將標準化矩陣乘以矩陣權重
繪圖
plt.figure()target_names = load_iris.target_names
y = load_iris.targetfor c, i, target_name in zip("rgb", [0, 1, 2], target_names):
plt.scatter(Y[y==i,0], Y[y==i,1], c=c, label=target_name)plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.legend()
plt.title('PCA')
plt.show()
Iris數據的主成分分析示意圖
矩陣分解
矩陣分解在機器學習中也至關重要,該過程本質上是將矩陣分解為矩陣的乘積。
常用的矩陣分解技術有LU分解,奇異值分解(SVD)等。
奇異值分解(SVD)
SVD可用于減小數據維度,奇異值分解如下:
令M為矩陣,其可以分解為三個矩陣的乘積,即正交矩陣(U),對角矩陣(S)和正交矩陣(V)的轉置。
結論
機器學習和深度學習是建立在數學概念之上的,掌握理解數學知識對于算法構建和數據處理有極大幫助。
線性代數的研究包括向量及其操作。在機器學習中,各處可見線性代數的背影,如線性回歸,獨熱編碼,主成分分析PCA,推薦系統中的矩陣分解。
深度學習更甚,其完全基于線性代數和微積分。梯度下降,隨機梯度下降等優化方法也建立在此之上。
矩陣是線性代數中的重要概念,通過矩陣可以緊湊地表示線性方程組、線性映射等。同樣,向量也是重要的概念,將不同向量與標量乘積進行加和可以組成不同的向量空間。
歡迎在評論區回復你的看法,我會虛心接受并進行改進。
免責聲明:本文中表達的觀點僅為作者個人觀點,不(直接或間接)代表卡耐基梅隆大學或與作者相關的其他組織。我知道,本文不盡完善,僅是本人當前的一些看法與思考,希望對讀者有所幫助。
資源
Google colab implementation.
Github repository
參考
[1] Linear Algebra, Wikipedia, https://en.wikipedia.org/wiki/Linear_algebra
[2] Euclidean Space, Wikipedia, https://en.wikipedia.org/wiki/Euclidean_space
[3] High-dimensional Simplexes for Supermetric Search, Richard Connor, Lucia Vadicamo, Fausto Rabitti, ResearchGate, https://www.researchgate.net/publication/318720793_High-Dimensional_Simplexes_for_Supermetric_Search
[4] ML | Normal Equation in Linear Regression, GeeksforGeeks, https://www.geeksforgeeks.org/ml-normal-equation-in-linear-regression/
[5] Vector Norms by Roger Crawfis, CSE541 — Department of Computer Science, Stony Brook University, https://www.slideserve.com/jaimie/vector-norms
[6] Variance Estimation Simulation, Online Stat Book by Rice University, http://onlinestatbook.com/2/summarizing_distributions/variance_est.html
[7] Lecture 17: Orthogonality, Oliver Knill, Harvard University, http://people.math.harvard.edu/~knill/teaching/math19b_2011/handouts/math19b_2011.pdf
[8] Orthonormality, Wikipedia, https://en.wikipedia.org/wiki/Orthonormality
[9] Linear Algebra/Basis, Wikibooks, https://en.wikibooks.org/wiki/Linear_Algebra/Basis
[10] Linear Algebra, LibreTexts, https://math.libretexts.org/Bookshelves/Linear_Algebra
- 免責聲明
- 本文所包含的觀點僅代表作者個人看法,不代表新火種的觀點。在新火種上獲取的所有信息均不應被視為投資建議。新火種對本文可能提及或鏈接的任何項目不表示認可。 交易和投資涉及高風險,讀者在采取與本文內容相關的任何行動之前,請務必進行充分的盡職調查。最終的決策應該基于您自己的獨立判斷。新火種不對因依賴本文觀點而產生的任何金錢損失負任何責任。





 新火種
2023-10-27
新火種
2023-10-27