新火種
2024-05-20 
華為最新研究挑戰ScalingLaw
“Scaling Law不是萬金油”——關于大模型表現，華為又提出了新理論。
他們發現，一些現象無法用Scaling Law來解釋，進而開展了更加深入的研究。
根據實驗結果，他們認為Transformer模型的成績，與記憶力高度相關。
具體來說，他們發現Scaling Law的缺陷主要有這兩種表現：
一是一些小模型的表現和大一些的模型相當甚至更好，如參數量只有2B的MiniCPM，表現與13B的Llama接近。
二是在訓練大模型時，如果過度訓練，模型表現不會繼續增加，反而呈現出了U型曲線。
經過深入研究和建模，團隊結合了Hopfield聯想記憶模型，提出了大模型表現的新解釋。
有人評價說，聯想記憶是人類所使用的一種記憶方法，現在發現大模型也會用，可以說是AI理解力的躍遷。
不過需要指出的是，這項研究雖有挑戰之意，但并非對Scaling Law的否定，而是對其局限性的客觀思考和重要補充，同時作者對前者的貢獻也做出了肯定。
構建全新能量函數
作者首先進行了假設，提出了新的能量函數，并根據Transformer模型的分層結構，設計了全局能量函數。
能量函數是一種描述系統狀態的數學工具，它將系統的每個可能狀態映射到一個實數值，函數值越低系統越“穩定”。
可以簡單地說，大模型的訓練過程就是在尋找能量函數的最小值。
具體到本文，作者提出了這樣的能量函數，其中x表示查詢向量，ρi表示記憶：
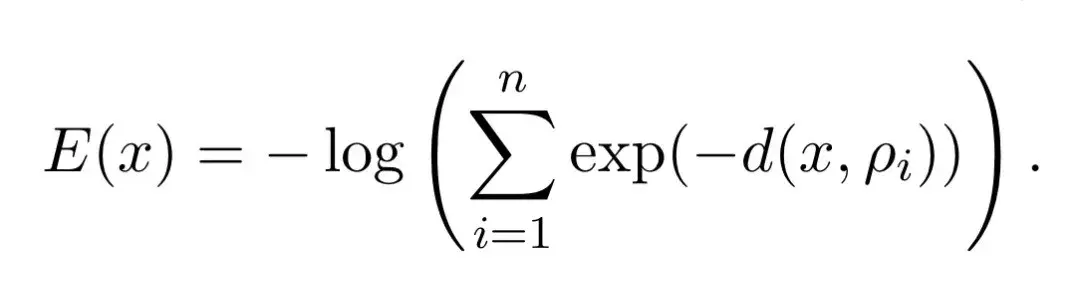
根據數學規律不難看出，當x與所有ρi的距離d(x, ρi)都很大時，每一項exp(-d(x, ρi))都會趨近于0，進而導致E(x)趨近于正無窮。
所以，E(x)在記憶向量ρi附近取得較小值，在遠離所有記憶的地方取得較大值，因此最小化E(x)就相當于找到與x最相似的記憶。
作者進一步證明，E(x)與現代連續Hopfield網絡（MCHN）的能量函數在數學形式上是等價的。
（Hopfield網絡是一種經典的聯想記憶神經網絡模型，由物理學家John Hopfield在1982年提出。）
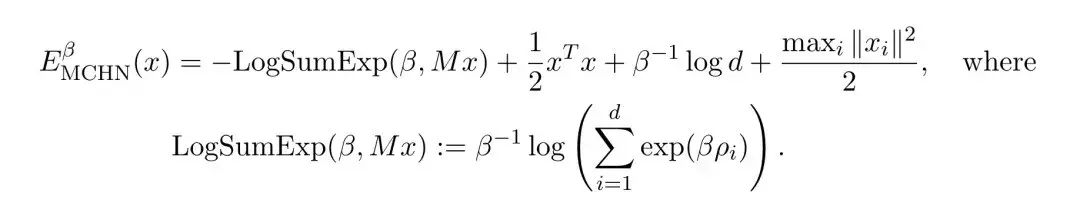
這兩個函數的相似性，可以通過下圖更加直觀地展現：
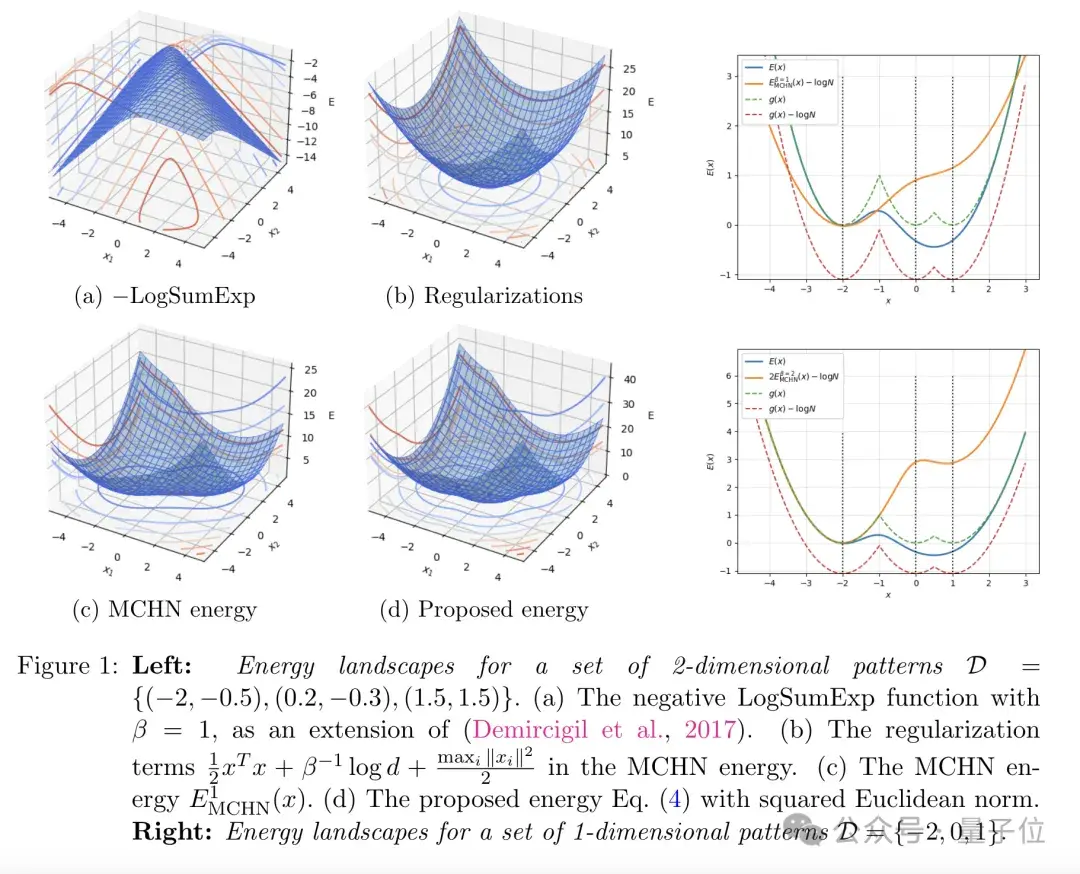
不過需要注意的是，Transformer通常由多個相同的注意力層堆疊而成，為了刻畫整個網絡的行為，有必要設計一個全局的能量函數。
作者借鑒了majorization-minimization（優化-最小化）的思想，將每一層的能量函數E_t(x)視為全局能量E_global(x)的一個緊上界。
于是，前向傳播的過程可以被視為依次最小化每一個E_t(x)，進而最小化E_global(x)。
通過巧妙地設計各層的能量函數使其互為緊上界（一個函數在另一個函數之上，但兩者非常接近），讓每層的局部能量函數都緊緊“束縛”住全局能量函數，作者構建出一個連貫的、可優化的全局能量函數，成功刻畫了Transformer的分層結構。
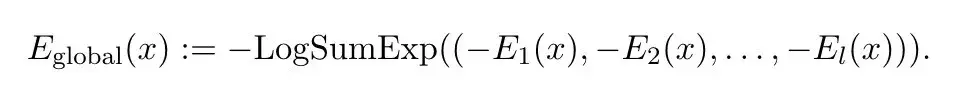大模型表現，記憶是關鍵為了驗證這些假設，研究人員開展了一系列實驗。
首先，作者在預訓練的GPT-2模型上對記憶力進行了分析。
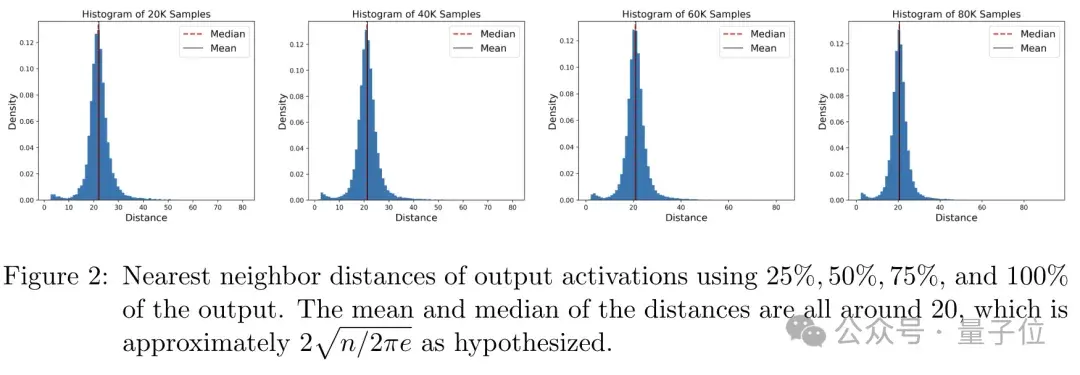
他們分析了模型最后一層的輸出表示與訓練樣本之間的關系，并計算了每個輸出向量與其最近訓練樣本的距離，繪制出了這些距離的分布直方圖。
結果表明，大多數輸出向量都集中在以訓練樣本為中心的局部區域內，距離中心大約10個單位。
這個結果與作者基于能量函數得出的理論預測（最優記憶半徑約為√(n/2πe)）非常接近。
這說明，Transformer的每一層都在進行一種基于相似性的記憶檢索，其性能主要取決于記憶半徑的大小。
進一步地，作者又在不同數據規模上訓練了GPT-2，并分析損失函數變化。
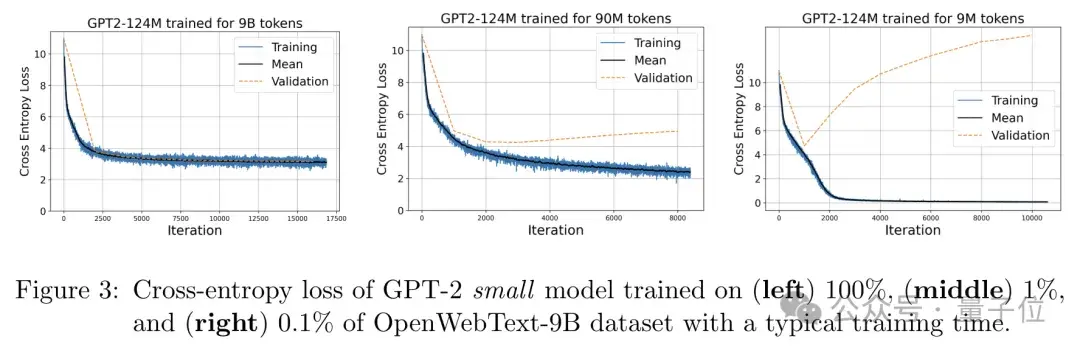
作者在三個不同規模（100%、1%、0.1%）的OpenWebText數據集上訓練了GPT-2模型，并記錄了其訓練和驗證損失的變化曲線。
實驗結果表明，當數據規模很小時，模型很容易過擬合，表現為訓練損失迅速下降到0，而驗證損失卻居高不下；
當數據規模較大時，訓練和驗證損失則接近且平穩，最終都顯著高于0。
也就是說，當數據規模足夠大、模型可以很好地“記憶”訓練集時，其最終的損失會穩定在理論預測的下界附近，從另一個角度說明了模型的性能確實主要取決于其記憶容量。
最后，作者又在問答數據集上訓練了原始Transformer，同時也分析了損失函數變化。
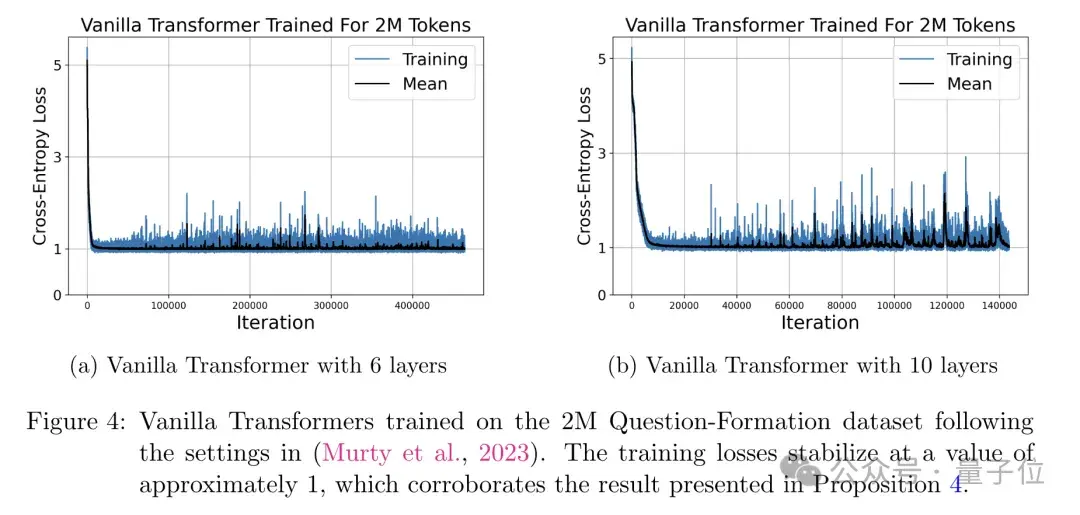
具體來說，他們在一個受控的任務（將聲明句改寫為疑問句）上訓練了一個純Transformer模型。
他們發現，隨著訓練的進行，模型的損失函數呈現出明顯的分段下降趨勢，每個階段對應于一定數量的訓練樣本被記憶，最終穩定在了理論預測的下界附近。
這個實驗不僅驗證了作者關于損失下界的理論預測，也直觀地展示了Transformer通過逐層能量最小化來實現記憶的過程。
總之，通過理論建模和多項實驗驗證，作者最終得出結論，Transformer的性能主要取決于其記憶訓練樣本的能力。
同時根據構建并被驗證的全局能量函數，作者還指出，為達到最優性能，模型參數量應隨訓練數據量的平方而線性增長。
如果你認為對你有所啟發，不妨閱讀原論文了解更多細節。
Tags:
相關推薦
- 免責聲明
- 本文所包含的觀點僅代表作者個人看法，不代表新火種的觀點。在新火種上獲取的所有信息均不應被視為投資建議。新火種對本文可能提及或鏈接的任何項目不表示認可。 交易和投資涉及高風險，讀者在采取與本文內容相關的任何行動之前，請務必進行充分的盡職調查。最終的決策應該基于您自己的獨立判斷。新火種不對因依賴本文觀點而產生的任何金錢損失負任何責任。
