九九热视频精品在线_国产成人mv视频在线观看_国产精品三级一区二区_亚洲精品国产av成拍色拍婷婷_久久伊人一区二区_国产高清精品网站_九九99热久久精品离线6_国产在线一卡2卡三卡4卡免费_日韩美女乱淫aaa高清视频_亚洲大胆_啪啪一级视频_午夜av免费观看_国产高清精品福利私拍国产写真_亚洲婷婷五月综合狠狠_日韩欧美一区二区三区视频_岛国av免费看_精品国产乱码久久久久久久软件_亚洲国产成人精品无码区99_www日本色_免费黄色看片

選自github.io作者：Manas Sahni機(jī)器之心編譯參與：魔王

使用深度學(xué)習(xí)庫可以大幅加速CNN模型運(yùn)行，那么這些庫中的哪些具體的做法實(shí)現(xiàn)了這種高速度和高性能呢？佐治亞理工學(xué)院計(jì)算機(jī)科學(xué)碩士研究生Manas Sahni在自己的電腦上試驗(yàn)了多種方法的策略，深入剖析高速卷積的實(shí)現(xiàn)過程。我的筆記本電腦CPU還可以，在TensorFlow等庫的加持下，這臺計(jì)算機(jī)可以在 10-100 毫秒內(nèi)運(yùn)行大部分常見CNN模型。2019年，即使是智能手機(jī)也能在不到半秒內(nèi)運(yùn)行「重量級」CNN模型。而當(dāng)我自己做了一個簡單的卷積層實(shí)現(xiàn)，發(fā)現(xiàn)這一個層的運(yùn)行時(shí)間竟然超過2秒時(shí)，我非常震驚。大家都知道，現(xiàn)代深度學(xué)習(xí)庫對大部分運(yùn)算具備高度優(yōu)化的生產(chǎn)級實(shí)現(xiàn)。但是這些庫使用了哪些人類不具備的「黑魔法」呢？它們?nèi)绾螌⑿阅芴嵘?00倍？當(dāng)它們「優(yōu)化」或加速神經(jīng)網(wǎng)絡(luò)運(yùn)算時(shí)，它們在做什么？當(dāng)談及高性能/高效DNN時(shí)，我常常問（或被問及）這些問題。本文嘗試介紹在DNN庫中如何實(shí)現(xiàn)一個卷積層。卷積不僅是很多DNN模型中最常見和最繁重的操作，它也是導(dǎo)致上述高性能實(shí)現(xiàn)的代表性trick：一點(diǎn)點(diǎn)算法智慧 + 大量調(diào)參 + 充分利用低級架構(gòu)。本文所涉及的很多內(nèi)容來自這篇開創(chuàng)性論文《Anatomy of High-Performance Matrix Multiplication》，這篇論文形成了線性代數(shù)庫（如OpenBLAS）所用算法的基礎(chǔ)；本文還涵蓋 Stefan Hadjis 博士和 Chris Rose的教程。

樸素卷積（Naive Convolution）不成熟的優(yōu)化是萬惡之源。——Donald Knuth在探討優(yōu)化之前，我們先來了解一下基線和瓶頸。這里是一個樸素 numpy/for-loop 卷積：'''Convolve `input` with `kernel` to generate `output` input.shape = [input_channels, input_height, input_width] kernel.shape = [num_filters, input_channels, kernel_height, kernel_width] output.shape = [num_filters, output_height, output_width]'''for filter in0..num_filters for channel in0..input_channels for out_h in0..output_height for out_w in0..output_width for k_h in0..kernel_height *for* k_w *in* 0..kernel_width output[filter, channel, out_h, out_h] += kernel[filter, channel, k_h, k_w] * input[channel, out_h + k_h, out_w + k_w]這個卷積包含6個嵌套的for loop，這里不涉及步幅（stride）、擴(kuò)張（dilation）等參數(shù)。假如這是MobileNet第一層的規(guī)模，我們在純C中運(yùn)行該層，花費(fèi)的時(shí)間竟然高達(dá)22秒！在使用最強(qiáng)悍的編譯器優(yōu)化后（如-O3 或 -Ofast），該卷積層的運(yùn)行時(shí)間降至2.2秒。但是就一個層而言，這個速度仍然太慢了。那么如果我使用Caffe運(yùn)行這個層呢？在同一臺計(jì)算機(jī)上使用Caffe運(yùn)行同一個層所花費(fèi)的時(shí)間僅為18毫秒，實(shí)現(xiàn)了100倍的加速！整個網(wǎng)絡(luò)運(yùn)行時(shí)間才大約100毫秒。那么「瓶頸」是什么？我們應(yīng)該從哪兒開始優(yōu)化呢？最內(nèi)的循環(huán)進(jìn)行了兩次浮點(diǎn)運(yùn)算（乘和加）。對于實(shí)驗(yàn)所使用的卷積層規(guī)模，它執(zhí)行了8516萬次，即該卷積需要1.7億次浮點(diǎn)運(yùn)算（170MFLOPs）。我的電腦CPU的峰值性能是每秒800億FLOPs，也就是說理論上它可以在0.002秒內(nèi)完成運(yùn)行。但是很明顯我們做不到，同樣很明顯的是，電腦的原始處理能力是非常充足的。理論峰值無法實(shí)現(xiàn)的原因在于，內(nèi)存訪問同樣需要時(shí)間：無法快速獲取數(shù)據(jù)則無法快速處理數(shù)據(jù)。上述高度嵌套的for-loop使得數(shù)據(jù)訪問非常艱難，從而無法充分利用緩存。貫穿本文的問題是：如何訪問正在處理的數(shù)據(jù)，以及這與數(shù)據(jù)存儲方式有何關(guān)聯(lián)。先決條件FLOP/s性能或者速度的度量指標(biāo)是吞吐量（throughput），即每秒浮點(diǎn)運(yùn)算數(shù)（FLoating Point Operations per Second，F(xiàn)LOP/s）。使用較多浮點(diǎn)運(yùn)算的大型運(yùn)算自然運(yùn)行速度較慢，因此FLOP/s是對比性能的一種較為可行的指標(biāo)。我們還可以用它了解運(yùn)行性能與CPU峰值性能的差距。我的計(jì)算機(jī)CPU具備以下屬性：2個物理內(nèi)核；每個內(nèi)核的頻率為2.5 GHz，即每秒運(yùn)行2.5×10^9個CPU循環(huán)；每個循環(huán)可處理32 FLOPs（使用AVX & FMA）。因此，該CPU的峰值性能為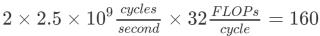：GFLOP/s。這就是我的CPU的理論峰值性能。類似地，我們可以得出單核CPU的峰值性能為80 GFLOP/s。存儲順序和行優(yōu)先邏輯上我們將矩陣/圖像/張量看作是多維度的，但實(shí)際上它們存儲在線性、一維的計(jì)算機(jī)內(nèi)存中。我們必須定義一個慣例，來規(guī)定如何將多個維度展開到線性一維存儲空間中，反之亦然。大部分現(xiàn)代深度學(xué)習(xí)庫使用行主序作為存儲順序。這意味著同一行的連續(xù)元素被存儲在相鄰位置。對于多維度而言，行主序通常意味著：在線性掃描內(nèi)存時(shí)第一個維度的變化速度最慢。那么維度本身的存儲順序呢？通常4維張量（如CNN中的張量）的存儲順序是NCHW、NHWC等。本文假設(shè)CNN中的張量使用NCHW存儲順序，即如果HxW 圖像的block為N，通道數(shù)為C，則具備相同N的所有圖像是連續(xù)的，同一block內(nèi)通道數(shù)C相同的所有像素是連續(xù)的，等等。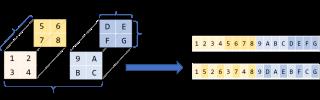Halide語言本文討論的優(yōu)化有時(shí)需要使用C語法甚至匯編語言這類底層的低級語言。這會影響代碼的可讀性，還會使嘗試不同優(yōu)化方法變得困難，因?yàn)樗枰貙懭看a。Halide是一種嵌入到 C++ 中的語言，它可以幫助抽象概念，旨在幫助用戶寫出快速的圖像處理代碼。它可以分離算法（需要計(jì)算的東西）和調(diào)度策略（如何計(jì)算算法以及何時(shí)計(jì)算），因此使用Halide試驗(yàn)不同優(yōu)化方法會更加簡便。我們可以保持算法不變，試用不用的調(diào)度策略。本文將使用Halide語言展示這些低級概念，但是你需要首先了解函數(shù)名稱。從卷積到矩陣相乘上文討論的樸素卷積已經(jīng)夠慢了，本節(jié)要介紹的實(shí)現(xiàn)則更加復(fù)雜，它包含步幅、擴(kuò)張、填充（padding）等參數(shù)。我們將繼續(xù)使用基礎(chǔ)卷積作為運(yùn)行示例，但是最大程度利用計(jì)算機(jī)的性能需要一些技巧——在多個層次上精心調(diào)參，以及充分利用所用計(jì)算機(jī)架構(gòu)的具體知識。換言之，解決所有難題是一項(xiàng)艱巨任務(wù)。那么我們可以將它轉(zhuǎn)換成容易解決的問題嗎？比如矩陣相乘。矩陣相乘（又稱matmul，或者Generalized Matrix Multiplication，GEMM）是深度學(xué)習(xí)的核心。全連接層、RNN等中都有它的身影，它還可用于實(shí)現(xiàn)卷積。卷積是濾波器和輸入圖像塊（patch）的點(diǎn)乘。如果我們將濾波器展開為2-D矩陣，將輸入塊展開為另一個2-D矩陣，則將兩個矩陣相乘可以得到同樣的數(shù)字。與CNN不同，近幾十年來矩陣相乘已經(jīng)得到廣泛研究和優(yōu)化，成為多個科學(xué)領(lǐng)域中的重要問題。將圖像塊展開為矩陣的過程叫做im2col（image to column）。我們將圖像重新排列為矩陣的列，每個列對應(yīng)一個輸入塊，卷積濾波器就應(yīng)用于這些輸入塊上。下圖展示了一個正常的3x3卷積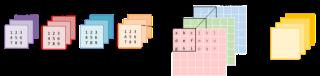：下圖展示的是該卷積運(yùn)算被實(shí)現(xiàn)為矩陣相乘的形式。右側(cè)的矩陣是im2col的結(jié)果，它需要從原始圖像中復(fù)制像素才能得以構(gòu)建。左側(cè)的矩陣是卷積的權(quán)重，它們已經(jīng)以這種形式儲存在內(nèi)存中。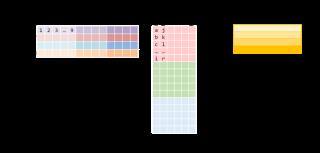注意，矩陣乘積直接得出了卷積輸出，無需額外「轉(zhuǎn)換」至原始形式。出于視覺簡潔考慮，此處將每個圖像塊作為獨(dú)立的個體進(jìn)行展示。而在現(xiàn)實(shí)中，不同圖像塊之間通常會有重疊，因而im2col可能導(dǎo)致內(nèi)存重疊。生成im2col 緩沖（im2col buffer）和過多內(nèi)存（inflated memory）所花費(fèi)的時(shí)間必須通過GEMM實(shí)現(xiàn)的加速來抵消。使用im2col可以將卷積運(yùn)算轉(zhuǎn)換為矩陣相乘。現(xiàn)在我們可以使用更加通用和流行的線性代數(shù)庫（如OpenBLAS、Eigen）對矩陣相乘執(zhí)行高效計(jì)算，而這是基于幾十年的優(yōu)化和微調(diào)而實(shí)現(xiàn)的。如果要抵消im2col變換帶來的額外工作和內(nèi)存，我們需要一些加速。接下來我們來看這些庫是如何實(shí)現(xiàn)此類加速的。本文還介紹了在系統(tǒng)級別進(jìn)行優(yōu)化時(shí)的一些通用方法。加速GEMM樸素本文剩余部分將假設(shè)GEMM按照該公式執(zhí)行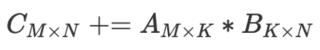：我們首先計(jì)算基礎(chǔ)標(biāo)準(zhǔn)矩陣相乘的時(shí)間：for i in0..M: for j in0..N: for k in0..K: C[i, j] += A[i, k] * B[k, j]使用Halide語言：Halide::Buffer C, A, B;Halide::Var x, y;C(x,y) += A(k, x) *= B(y, k); // loop bounds, dims, etc. are taken care of automatically最內(nèi)的代碼行做了2次浮點(diǎn)運(yùn)算（乘和加），代碼執(zhí)行了MNK次，因此該GEMM的FLOPs數(shù)為2MNK。下圖展示了不同矩陣大小對應(yīng)的性能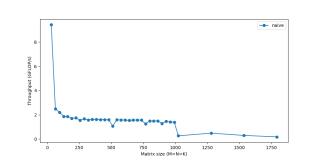：僅僅達(dá)到峰值性能的10%！接下來我們將探索加速計(jì)算的方式，但不變的主題仍然是：如果無法快速獲取數(shù)據(jù)，則僅僅快速計(jì)算數(shù)據(jù)并不足夠。隨著矩陣規(guī)模越來越大，內(nèi)存成為更加嚴(yán)重的問題，而性能也會繼續(xù)逐漸下降。你看到圖中的劇烈下跌了嗎？這表示當(dāng)矩陣太大無法適應(yīng)緩存時(shí)，吞吐量突然下跌。緩存RAM是大的存儲空間，但速度較慢。CPU緩存的速度要快得多，但其規(guī)模較小，因此恰當(dāng)?shù)厥褂肅PU緩存至關(guān)重要。但是并不存在明確的指令：「將該數(shù)據(jù)加載到緩存」。該過程是由CPU自動管理的。每一次從主內(nèi)存中獲取數(shù)據(jù)時(shí)，CPU會將該數(shù)據(jù)及其鄰近的數(shù)據(jù)加載到緩存中，以便利用訪問局部性（locality of reference）。你應(yīng)該首先注意到我們訪問數(shù)據(jù)的模式。我們按照下圖A的形式逐行遍歷數(shù)據(jù)，按照下圖B的形式逐列遍歷數(shù)據(jù)。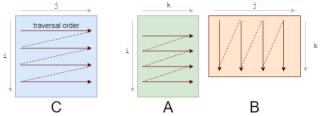它們的存儲也是行優(yōu)先的，因此一旦我們找到 A[i, k]，則它在該行中的下一個元素A[i, k+1]已經(jīng)被緩存了。接下來我們來看B中發(fā)生了什么：列的下一個元素并未出現(xiàn)在緩存中，即出現(xiàn)了緩存缺失（cache miss）。這時(shí)盡管獲取到了數(shù)據(jù)，CPU也出現(xiàn)了一次停頓。獲取數(shù)據(jù)后，緩存同時(shí)也被 B 中同一行的其他元素填滿。我們實(shí)際上并不會使用到它們，因此它們很快就會被刪除。多次迭代后，當(dāng)我們需要那些元素時(shí)，我們將再次獲取它們。我們在用實(shí)際上不需要的值污染緩存。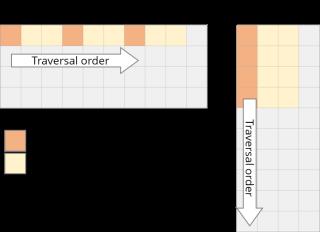我們需要重新修改loop，以充分利用緩存能力。如果數(shù)據(jù)被讀取，則我們要使用它。這就是我們所做的第一項(xiàng)改變：循環(huán)重排序（loop reordering）。我們將i,j,k 循環(huán)重新排序?yàn)?i,k,j：for i in0..M: for k in0..K: for j in0..N:答案仍然是正確的，因?yàn)槌?加的順序?qū)Y(jié)果沒有影響。而遍歷順序則變成了如下狀態(tài)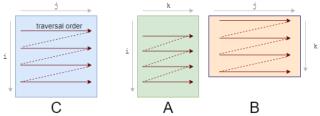：循環(huán)重排序這一簡單的變化，卻帶來了相當(dāng)可觀的加速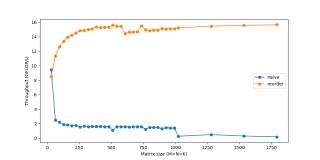：平鋪（Tiling）要想進(jìn)一步改進(jìn)重排序，我們需要考慮另一個緩存問題。對于A中的每一行，我們針對B中所有列進(jìn)行循環(huán)。而對于 B 中的每一步，我們會在緩存中加載一些新的列，去除一些舊的列。當(dāng)?shù)竭_(dá)A的下一行時(shí)，我們?nèi)耘f重新從第一列開始循環(huán)。我們不斷在緩存中添加和刪除同樣的數(shù)據(jù)，即緩存顛簸（cache thrashing）。如果所有數(shù)據(jù)均適應(yīng)緩存，則顛簸不會出現(xiàn)。如果我們處理的是小型矩陣，則它們會舒適地待在緩存里，不用經(jīng)歷重復(fù)的驅(qū)逐。慶幸的是，我們可以將矩陣相乘分解為子矩陣。要想計(jì)算 C 的r×c平鋪，我們僅需要A的r行和B的c列。接下來，我們將 C 分解為6x16的平鋪：C(x, y) += A(k, y) * B(x, k);C.update().tile(x, y, xo, yo, xi, yi, 6, 16)/*in pseudocode:for xo in 0..N/16: for yo in 0..M/6: for yi in 6: for xi in 0..16: for k in 0..K: C(...) = ...*/我們將x,y 維度分解為外側(cè)的xo,yo和內(nèi)側(cè)的xi,yi。我們將為該6x16 block優(yōu)化micro-kernel（即xi,yi），然后在所有block上運(yùn)行micro-kernel（通過xo,yo進(jìn)行迭代）。向量化 & FMA大部分現(xiàn)代CPU支持SIMD（Single Instruction Multiple Data，單指令流多數(shù)據(jù)流）。在同一個CPU循環(huán)中，SIMD可在多個值上同時(shí)執(zhí)行相同的運(yùn)算/指令（如加、乘等）。如果我們在4個數(shù)據(jù)點(diǎn)上同時(shí)運(yùn)行SIMD指令，就會直接實(shí)現(xiàn)4倍的加速。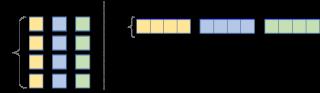因此，當(dāng)我們計(jì)算處理器的峰值速度時(shí)，我們其實(shí)有些作弊，把該向量化性能作為峰值性能。對于向量等數(shù)據(jù)而言，SIMD用處多多，在處理此類數(shù)據(jù)時(shí)，我們必須對每一個向量元素執(zhí)行同樣的指令。但是我們?nèi)匀恍枰O(shè)計(jì)計(jì)算核心，以充分利用它。計(jì)算峰值FLOPs時(shí)，我們所使用的第二個技巧是FMA（Fused Multiply-Add）。盡管乘和加是兩種獨(dú)立的浮點(diǎn)運(yùn)算，但它們非常常見，有些專用硬件單元可以將二者融合為一，作為單個指令來執(zhí)行。編譯器通常會管理FMA的使用。在英特爾CPU上，我們可以使用SIMD（AVX & SSE）在單個指令中處理多達(dá)8個浮點(diǎn)數(shù)。編譯器優(yōu)化通常能夠獨(dú)自識別向量化的時(shí)機(jī)，但是我們需要掌控向量化以確保無誤。C.update().tile(x, y, xo, yo, xi, yi, 6, 16).reorder(xi, yi, k, xo, yo).vectorize(xi, 8)/*in pseudocode:for xo in 0..N/16: for yo in 0..M/6: for k in 0..K: for yi in 6: for vectorized xi in 0..16: C(...) = ...*/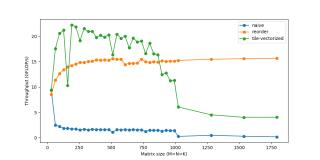多線程處理（Threading）到現(xiàn)在為止，我們僅使用了一個CPU內(nèi)核。我們擁有多個內(nèi)核，每個內(nèi)核可同時(shí)執(zhí)行多個指令。一個程序可被分割為多個線程，每個線程在單獨(dú)的內(nèi)核上運(yùn)行。C.update().tile(x, y, xo, yo, xi, yi, 6, 16).reorder(xi, yi, k, xo, yo).vectorize(xi, 8).parallel(yo)/*in pseudocode:for xo in 0..N/16 in steps of 16: for parallel yo in steps of 6: for k in 0..K: for yi in 6: for vectorized xi in 0..16 in steps of 8: C(...) = ...*/你可能注意到，對于非常小的規(guī)模而言，性能反而下降了。這是因?yàn)楣ぷ髫?fù)載很小，線程花費(fèi)較少的時(shí)間來處理工作負(fù)載，而花費(fèi)較多的時(shí)間同步其他線程。多線程處理存在大量此類問題。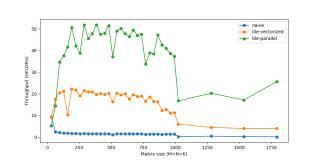展開（Unrolling）循環(huán)使我們避免重復(fù)寫同樣代碼的痛苦，但同時(shí)它也引入了一些額外的工作，如檢查循環(huán)終止、更新循環(huán)計(jì)數(shù)器、指針運(yùn)算等。如果手動寫出重復(fù)的循環(huán)語句并展開循環(huán)，我們就可以減少這一開銷。例如，不對1個語句執(zhí)行8次迭代，而是對4個語句執(zhí)行2次迭代。這種看似微不足道的開銷實(shí)際上是很重要的，最初意識到這一點(diǎn)時(shí)我很驚訝。盡管這些循環(huán)操作可能「成本低廉」，但它們肯定不是免費(fèi)的。每次迭代2-3個額外指令的成本會很快累積起來，因?yàn)榇颂幍牡螖?shù)是數(shù)百萬。隨著循環(huán)開銷越來越小，這種優(yōu)勢也在不斷減小。展開是幾乎完全被編譯器負(fù)責(zé)的另一種優(yōu)化方式，除了我們想要更多掌控的micro-kernel。C.update().tile(x, y, xo, yo, xi, yi, 6, 16).reorder(xi, yi, k, xo, yo).vectorize(xi, 8).unroll(xi).unroll(yi)/*inpseudocode:for xo in0..N/16: for parallel yo:for k in0..K: C(xi:xi+8, yi+0) C(xi:xi+8, yi+1) ... C(xi:xi+8, yi+5) C(xi+8:xi+16, yi+0) C(xi+8:xi+16, yi+1) ... C(xi+8:xi+16, yi+5)*/現(xiàn)在我們可以將速度提升到接近60 GFLOP/s。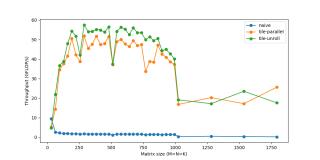總結(jié)上述步驟涵蓋一些性能加速最常用的變換。它們通常以不同方式組合，從而得到更加復(fù)雜的調(diào)度策略來計(jì)算同樣的任務(wù)。下面就是用Halide語言寫的一個調(diào)度策略：matrix_mul(x, y) += A(k, y) * B(x, k); out(x, y) = matrix_mul(x, y);out.tile(x, y, xi, yi, 24, 32) .fuse(x, y, xy).parallel(xy) .split(yi, yi, yii, 4) .vectorize(xi, 8) .unroll(xi) .unroll(yii); matrix_mul.compute_at(out, yi) .vectorize(x, 8).unroll(y); matrix_mul.update(0) .reorder(x, y, k) .vectorize(x, 8) .unroll(x) .unroll(y) .unroll(k, 2);它執(zhí)行了：將out分解為32x24的平鋪，然后將每個平鋪進(jìn)一步分解為8x24的子平鋪。使用類似的重排序、向量化和展開，在臨時(shí)緩沖區(qū)（matrix_mul）計(jì)算8x24 matmul。使用向量化、展開等方法將臨時(shí)緩沖區(qū)matrix_mul 復(fù)制回out。在全部32x24平鋪上并行化這一過程。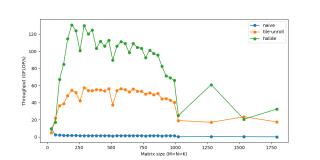最后，我們將速度提升至超過120 GFLOPs，接近峰值性能160 GFLOPs，堪比OpenBLAS等生產(chǎn)級庫。使用im2col類似的微調(diào)代碼和矩陣相乘，同樣的卷積可以在大約20毫秒內(nèi)完成運(yùn)行。如想深入了解，你可以嘗試自行試驗(yàn)不同的調(diào)度策略。作為一名工程師，我經(jīng)常聽到關(guān)于緩存、性能等的語句，而親眼看到它們的實(shí)際效果是非常有趣和值得的。注意：im2col+gemm方法是大部分深度學(xué)習(xí)庫中流行的通用方法。但是，對于特定的常用規(guī)模、不同的架構(gòu)（GPU）和不同的運(yùn)算參數(shù)（如擴(kuò)張、分組等），專門化（specialization）是關(guān)鍵。這些庫可能也有更專門化的實(shí)現(xiàn)，這些實(shí)現(xiàn)利用類似的trick或具體的假設(shè)。經(jīng)過不斷試錯的高度迭代過程之后，我們構(gòu)建了這些micro-kernel。對于什么方法效果好/不好、必須基于結(jié)果考慮注釋，程序員通常只有直觀的想法。聽起來和深度學(xué)習(xí)研究差不多，不是嗎？