九九热视频精品在线_国产成人mv视频在线观看_国产精品三级一区二区_亚洲精品国产av成拍色拍婷婷_久久伊人一区二区_国产高清精品网站_九九99热久久精品离线6_国产在线一卡2卡三卡4卡免费_日韩美女乱淫aaa高清视频_亚洲大胆_啪啪一级视频_午夜av免费观看_国产高清精品福利私拍国产写真_亚洲婷婷五月综合狠狠_日韩欧美一区二区三区视频_岛国av免费看_精品国产乱码久久久久久久软件_亚洲国产成人精品无码区99_www日本色_免费黄色看片

選自machinelearningmastery

作者：Jason Brownlee

機器之心編譯

編譯：高璇，Geek AI

要說誰是當下最火的生成模型，GAN 當之無愧！然而，模式坍塌、訓練不穩定等問題嚴重制約著 GAN 家族的發展。為了提圖像質量、樣本多樣性的角度量化評價 GAN 模型的性能，研究者們提出了一系列度量指標，其中 FID 就是近年來備受關注的明星技術，本文將詳細介紹如何在 python 環境下實現 Frechet Inception 距離（FID）。

Frechet Inception 距離得分（Frechet Inception Distance score，FID）是計算真實圖像和生成圖像的特征向量之間距離的一種度量。

FID 從原始圖像的計算機視覺特征的統計方面的相似度來衡量兩組圖像的相似度，這種視覺特征是使用 Inception v3 圖像分類模型計算的得到的。分數越低代表兩組圖像越相似，或者說二者的統計量越相似，FID 在最佳情況下的得分為 0.0，表示兩組圖像相同。

FID 分數被用于評估由生成性對抗網絡生成的圖像的質量，較低的分數與較高質量的圖像有很高的相關性。

在本教程中，你將了解如何通過 FID 評估生成的圖像。

同時你還將了解：

在本文作者有關 GAN 的新書中，讀者可以了解到如何使用 Keras 開發 DCGAN、條件 GAN、Pix2Pix、CycleGAN 等對抗生成網絡，書中還提供 29 個詳細教程和完整源代碼。

下面進入正文部分：

教程概述

本教程分為五個部分，分別是：

機器之心整理了前三部分的代碼，感興趣的讀者可以在原文中查看 Keras 的 FID 實現和計算真實圖像 FID 的方法。

何為 FID？

Frechet Inception 距離（FID）是評估生成圖像質量的度量標準，專門用于評估生成對抗網絡的性能。

FID 分數由 Martin Heusel 等人于 2017 年在論文「GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium」（https://arxiv.org/abs/1706.08500017）中提出并使用。該分數作為對現有的 Inception 分數（IS）的改進而被提出。

為了評估 GAN 在圖像生成任務中的性能，我們引入了「Frechet Inception Distance」（FID），它能比 Inception 分數更好地計算生成圖像與真實圖像的相似性。——「GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium」（https://arxiv.org/abs/1706.08500）, 2017.

Inception 分數基于目前性能最佳的圖像分類模型 Inception v3 對一組合成圖像的分類情況（將其分類為 1,000 類對象中的一種）來評估圖像的質量。該分數結合了每個合成圖像的條件類預測的置信度（質量）和預測類別的邊緣概率積分（多樣性）。

Inception 分數缺少合成圖像與真實圖像的比較。研發 FID 分數的目的是基于一組合成圖像的統計量與來自目標域的真實圖像的統計量進行的比較，實現對合成圖像的評估。

Inception 分數的缺點是沒有使用現實世界樣本的統計量，并將其與合成樣本的統計量進行比較。——「GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium 」（https://arxiv.org/abs/1706.08500）, 2017.

與 Inception 分數一樣，FID 分數也使用了 Inception v3 模型。具體而言，模型的編碼層（圖像的分類輸出之前的最后池化層）被用來抽取輸入圖像的用計算機視覺技術指定的特征。這些激活函數是針對一組真實圖像和生成圖像計算的。

通過計算圖像的均值和協方差，將激活函數的輸出歸納為一個多變量高斯分布。然后將這些統計量用于計算真實圖像和生成圖像集合中的激活函數。

然后使用 Frechet 距離（又稱 Wasserstein-2 距離）計算這兩個分布之間的距離。

兩個高斯分布（合成圖像和真實圖像）的差異由 Frechet 距離（又稱 Wasserstein-2 距離）測量。——「GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium」（https://arxiv.org/abs/1706.08500）, 2017.

使用來自 Inception v3 模型的激活函數輸出來歸納每個圖像，得分即為「Frechet Inception Distance」。

FID 越低，圖像質量越好；反之，得分越高，質量越差，兩者關系應該是線性的。

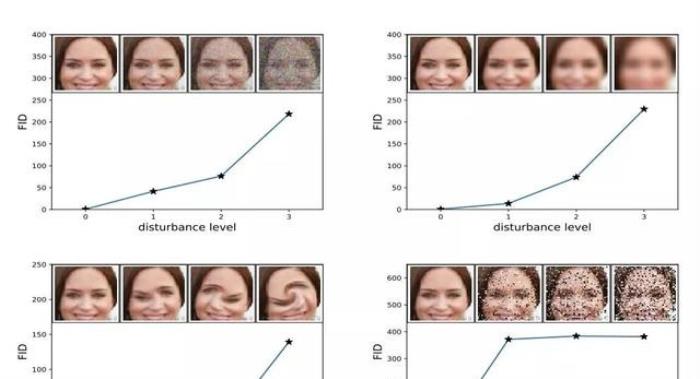
該分數的提出者表明，當應用系統失真（如加入隨機噪聲和模糊）時，FID 越低，圖像質量越好。

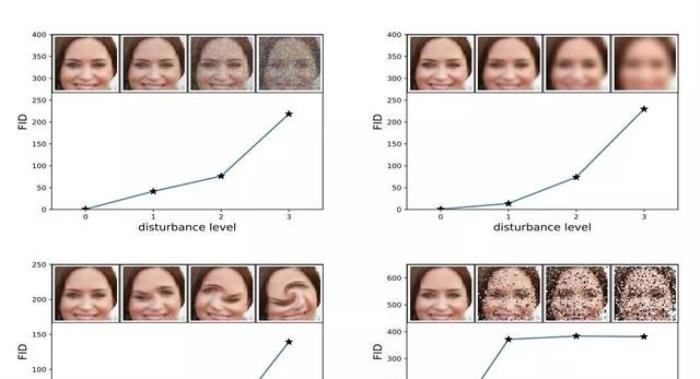
圖像失真程度的提高與高 FID 分數之間的關系。

如何計算 Frechet Inception 距離？

首先，通過加載經過預訓練的 Inception v3 模型來計算 FID 分數。

刪除模型原本的輸出層，將輸出層換為最后一個池化層（即全局空間池化層）的激活函數輸出值。此輸出層有 2,048 維的激活向量，因此，每個圖像被預測為 2,048 個激活特征。該向量被稱為圖像的編碼向量或特征向量。

針對一組來自問題域的真實圖像，預測 2,048 維的特征向量，用來提供真實圖像表征的參考。然后可以計算合成圖像的特征向量。

結果就是真實圖像和生成圖像各自的 2,048 維特征向量的集合。

然后使用以下公式計算 FID 分數：

該分數被記為 d^2，表示它是一個有平方項的距離。

「mu_1」和「mu_2」指的是真實圖像和生成圖像的特征均值（例如，2,048 維的元素向量，其中每個元素都是在圖像中觀察到的平均特征）。

C_1 和 C_2 是真實圖像的和生成圖像的特征向量的協方差矩陣，通常被稱為 sigma。

|| mu_1-mu_2 ||^2 代表兩個平均向量差的平方和。Tr 指的是被稱為「跡」的線性代數運算（即方陣主對角線上的元素之和）。

sqrt 是方陣的平方根，由兩個協方差矩陣之間的乘積給出。

矩陣的平方根通常也被寫作 M^（1/2），即矩陣的 1/2 次方。此運算可能會失敗，由于該運算是使用數值方法求解的，是否成功取決于矩陣中的值。通常，所得矩陣中的一些元素可能是虛數，它們通常可以被檢測出來并刪除。

如何用 NumPy 實現 Frechet Inception 距離？

使用 NumPy 數組在 Python 中實現 FID 分數的計算非常簡單。

首先，讓我們定義一個函數，它將為真實圖像和生成圖像獲得一組激活函數值，并返回 FID 分數。

下面列出的「calculate_fid()」函數實現了該過程。

通過該函數，我們幾乎直接實現了 FID 分數的計算。值得注意的是，TensorFlow 中的官方實現計算元素的順序稍有不同（可能是為了提高效率），并在加入了矩陣平方根附近的額外檢查，以處理可能的數值不穩定性。

如果在自己的數據集上計算 FID 時遇到問題，我建議你查看官方教程并擴展下面的實現，以添加這些檢查。

def calculate_fid(act1, act2):

# calculate mean and covariance statistics

mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False)

mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False)

# calculate sum squared difference between means

ssdiff = numpy.sum((mu1 - mu2)*2.0)

# calculate sqrt of product between cov

covmean = sqrtm(sigma1.dot(sigma2))

# check and correct imaginary numbers from sqrt

if iscomplexobj(covmean):

covmean = covmean.real

# calculate score

fid = ssdiff + trace(sigma1 + sigma2 - 2.0 covmean)

return fid

接下來，我們可以測試這個函數來計算一些人造特征向量的 Inception 分數。

特征向量可能包含小的正值，長度為 2,048 個元素。我們可以用包含小隨機數的特征向量構建兩組圖像（每組 10 幅），如下所示：

act1 = random(102048)

act1 = act1.reshape((10,2048))

act2 = random(102048)

act2 = act2.reshape((10,2048))

一個測試是計算一組激活與其自身之間的 FID，我們期望分數為 0.0。

然后計算兩組隨機激活之間的距離，我們期望它們是一個很大的數字。

fid = calculate_fid(act1, act1)

print('FID (same): %.3f' % fid)

fid = calculate_fid(act1, act2)

print('FID (different): %.3f' % fid)

將所有這些結合在一起，完整的示例如下：

import numpy

from numpy import cov

from numpy import trace

from numpy import iscomplexobj

from numpy.random import random

from scipy.linalg import sqrtm

def calculate_fid(act1, act2):

# calculate mean and covariance statistics

mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False)

mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False)

# calculate sum squared difference between means

ssdiff = numpy.sum((mu1 - mu2)*2.0)

# calculate sqrt of product between cov

covmean = sqrtm(sigma1.dot(sigma2))

# check and correct imaginary numbers from sqrt

if iscomplexobj(covmean):

covmean = covmean.real

# calculate score

fid = ssdiff + trace(sigma1 + sigma2 - 2.0 covmean)

return fid

act1 = random(102048)

act1 = act1.reshape((10,2048))

act2 = random(102048)

act2 = act2.reshape((10,2048))

fid = calculate_fid(act1, act1)

print('FID (same): %.3f' % fid)

fid = calculate_fid(act1, act2)

print('FID (different): %.3f' % fid)

運行這段代碼示例，首先會顯示出激活函數值「act1」和它自己之間的 FID 分數，正如我們所預想的那樣，該值為 0.0（注：該分數的符號可以忽略）

同樣，正如我們所預料的，兩組隨機激活函數值之間的距離是一個很大的數字，在本例中為 358

FID (same): -0.000

FID (different): 358.927