深度學習如何學習直觀物理學
機器之心分析師網絡
作者:仵冀穎
編輯:Joni
從直觀物理學講起。
在這篇文章中我們討論的是一個對于非物理學專業的人來說相對陌生的概念 --- 直觀物理學(Intuitive Physics),我們聚焦的是深度學習是如何學習直觀物理學的。
首先,我們從究竟什么是直觀物理學談起。人類能夠了解自己所處的物理環境,并與環境中動態變化的物體和物質相互作用,對觀察到的事件發展趨勢做出近似性的預測(例如,預測投擲的球的軌跡、砍掉的樹枝將墜落的方向)。描述這些活動背后規律的知識就是直覺物理學。直覺物理學幾十年來一直是認知科學領域一個活躍的研究領域。近年來,隨著人工智能相關新理論方法的應用,直覺物理學研究重新煥發了活力。研究人員利用直覺物理學的模型模擬行為研究的結果,而這些行為研究將心理物理測量應用于復雜動態顯示的感知和推理。
圖 1 給出了幾個常見的直覺物理學問題示例 [1]。圖 1 中的任務是對各種情況下物體和物質的屬性或運動進行推理。除了物體碰撞判斷(A),通常通過物理系統的靜態圖來描述問題。在(B–D)中,不間斷線表征正確的軌跡,而間斷線表征常見的錯誤預測。概率模擬框架(Probabilistic simulation framework)成功地預測了人們對動態顯示中物體的屬性(A)和運動(C)的期望,以及兩個充液容器的澆注角度(F)。不過,人們在進行推理判斷時一般是根據不同的情況、不同的運動理論進行推理的。這導致人類感知和推理物理情況的能力普遍不高,尤其是在拋射物運動和物體碰撞的情況下。
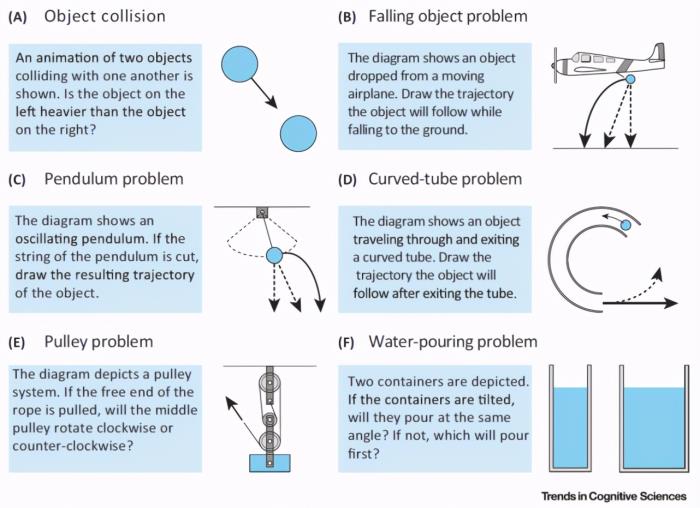
圖 1. 直覺物理學問題示例
在這一章中,我們介紹幾種直觀物理學的研究方法,啟發式方法、概率模擬模型和深度學習方法。如圖 2 所示。
圖 2. 確定兩個碰撞物體相對質量的三種計算方法的描述。模型之間的主要區別在于學習的作用(啟發式方法最小,概率模擬有限,深度學習比較大)。(A) 在啟發式模型中,假設觀測到的速度與環境中的物理速度相等(即直接感知速度)。比較碰撞后的速度,并假設碰撞后以最大速度移動的物體較輕。啟發式模型中沒有考慮學習的作用。(B) 概率模擬模型將先驗放在隱藏的物理變量上。運動先驗將感知速度偏向慢運動。通過比較模擬的最終速度和觀測的速度,確定不同質量比的可能性。學習可能會影響推理所涉及的先驗知識。(C) 在一個深度學習模型中,卷積神經網絡(CNN)被訓練成二維圖像的輸入和輸出對象屬性(質量和摩擦力)。然后使用 CNN 從先前看不見的圖像數據中預測對象屬性。這種方法使用了自下而上的學習過程。
除了涉及單個物體運動的研究外,早期關于兩個物體碰撞的研究還表明,根據牛頓原理,人類的判斷常常會偏離預期。例如,考慮一個初始運動物體(運動物體)與一個初始靜止物體(拋射物體)碰撞的情況。當運動物體對拋射物體的物理效應相對較小時(例如,拋射物體的碰撞后速度小于運動物體的碰撞前速度),人們做出的因果關系判斷會比物理效應大時更強烈(例如拋射物體的碰撞后速度大于機動物體的碰撞前速度)。這一發現被稱為啟發式方法(Heuristics ),也就是最經典的直觀物理學方法:人們可以根據顯著的知覺線索使用下面兩個規則來推斷碰撞物體的屬性。(i) 碰撞事件后移動較快的物體較輕(速度啟發式;如圖 2A 所示),(ii)以較大角度偏轉的物體較輕(角度啟發式)。然而,盡管這些啟發式方法在某些情況下解釋了人類對碰撞物體相對質量(Relative Mass)的判斷,但它們并不能推廣到其他情況。
啟發式方法其中一個難點,是顯性物理概念是如何從經驗中衍生出來的?以及它們與隱性物理知識的相互作用程度如何?這兩個核心問題還沒有確定答案。造成這種不確定性的一個原因似乎出自系統概念分類的困難,而這種困難源于物理環境中的知覺模糊性表述,或者任務中所涉及到的知覺以及任務中物理變量的無效表示。例如,當物體從搖錘中釋放后繪制其軌跡時,最直接的想法是“垂直向下運動(straight-down)”,因為物體在所示(靜態)位置的速度是模糊的。或者,人們會認為從運動物體上落下的物體會垂直向下運動,因為這種運動方式代表了物體相對于運動物體的感知運動。此外,這種問題在旋轉容器上繪制水位(即水位問題)時也會出現,即使已經明確指出了液體表面應保持水平而無需考慮容器的方向。此時,造成判斷偏差的原因是無效表示:使用軸平行于容器表面的以對象為中心的參照系。在這種不確定性下,人們對物理量的判斷(例如,兩個物體相互碰撞產生的力)與牛頓原理不一致。因此,直覺物理學方法應當能夠考慮到(i)認知結構和物理結構之間的對應關系,(ii)不同問題背景下認知表征的性質,(iii)物理近似在復雜顯示中的作用,(iv)預測判斷任務中顯性概念與隱性理解的交互作用。
近年來,基于貝葉斯推理(Bayesian inference)的新的理論方法,特別是噪聲牛頓框架(Noisy Newton Framework),使直覺物理學的研究重新煥發了活力,它將真實物理原理與感官信息的不確定性相結合。基于噪聲牛頓框架的模型假設,人們將帶噪聲的感官輸入與物理情境下的感知變量,以及物理變量的先驗信念(Prior Belief)相結合,并根據牛頓物理學對這些變量之間的約束進行建模。例如,在碰撞事件(Collision Event)中,通過模擬數千種物理情況來建模預測過程。在每個模擬過程中,使用牛頓定律對感知和物理特性的采樣變量進行計算而得到物理結果。盡管大多數感知變量都是可觀察的(例如速度、位置),但仍然有必要將客觀證據(觀察)轉化為主觀估計,方法是將噪聲感官輸入與感知線索統計規律的先驗值相結合。另外,一些物理性質(如質量、粘度)是不能直接觀察得到的,必須從感官觀察和 / 或物理世界的一般知識中推斷出來,如圖 2B 所示。
噪聲牛頓框架有效地調和了人類判斷和牛頓物理學之間的一些矛盾。在噪聲牛頓框架下,通過將噪聲信息傳遞給物理引擎來實現推理,物理引擎由物體碰撞時的動量守恒原理定義。在假設感知輸入到物理期望的轉換符合牛頓原理約束的前提下,有關對象動力學(Object dynamics )的知識被 “寫入” 模型。概率模擬模型(Probabilistic Simulation Model)的核心思想是人類構造關于物理情境的概率心理模型,通過心理模擬來推斷未來的物體狀態。心理模擬的作用得到了機械推理的支持,它證明了人們通過構造和轉換空間表征來回答關于物體和物質行為的問題,從而對物理系統進行推理。空間表征意味著物體在物理世界中的位置、運動和隱藏屬性以及它們之間的相互作用在大腦中可以進行概率學的編碼和表征。
最近的神經科學研究結果表明,心理模擬過程可以以概率論來描述,這些區域與大腦的 “多需求” 系統重疊。概率模擬模型通過將噪聲信息處理與先進的基于物理的圖形引擎相結合來模擬未來的對象狀態,從而在物理推理任務中做出判斷。在每個模擬中,場景中感知變量和物理變量的值根據模擬對象位置、速度和屬性的噪聲信息處理的分布進行采樣。基于感知和物理輸入的采樣狀態,使用近似牛頓原理的 “直觀物理引擎(Intuitive Physics Engine)” 來模擬未來的對象狀態。然后查詢每個模擬的結果以形成預測判斷,例如,是否有一個積木塔倒塌或有多少液體落入指定區域。最后,在模擬中聚合判斷以形成預測的響應分布。選擇仿真模型中的參數,使分布能夠準確反映人的行為。概率模擬模型建立在兩個基本組件上:作為物理引擎輸入的物理變量和引擎中編碼的物理原理。一些物理變量(如速度和物體位置)可以直接感知,盡管感知值可能會被神經噪聲和一般先驗(如運動感知中的緩慢平滑先驗)所扭曲。還有一些物理變量(如質量、粘度、密度和重力)是無法直接感知的,那么問題是,人類如何從視覺系統中的低級特征中推斷出這些物理屬性的?
深度學習模型的最新進展表明,一種潛在的計算機制可以從視覺輸入中推斷物理屬性,并對物理情況做出預測。這種方法出現在機器學習領域,是基卷積神經網絡(CNNs)實現的。卷積神經網絡以像素級編碼的圖像作為輸入,通過分層處理信息,學習從簡單的視覺成分(如邊緣)到更復雜的模式和對象類別的多層次抽象表示。具體的,一種混合方法(Hybrid approach)將基于知識的物理模型與基于學習的識別網絡相結合,用于從視覺輸入中預測物理屬性。這種混合方法在解釋人類直觀的物理預測能力方面取得了一些成功。如圖 2.C 中,利用深度學習網絡,通過多個處理層將動態視覺輸入(二維圖像序列)映射到兩個碰撞物體的推斷屬性(質量和摩擦力)。這一過程有效地逆轉了生成物理過程的一個關鍵組成部分。CNNs 基于與對象屬性相關的圖像數據進行訓練,對象屬性是通過將視覺輸入的關鍵特征與物理引擎的模擬輸出相匹配來確定的。CNNs 具有與人類相當的推斷能力,表明基于學習的方法可以有效地與基于知識的物理引擎集成,以推斷環境中物體的屬性和動力學。
由上面對直觀物理學的回顧可以看出,以概率模擬為基礎的物理推理方法一般都假定真實的物理原理是作為先驗知識提供的。從計算的角度來看,基于樣本(Exemplar)的方法可以將物理情況的觀察實例表示為與相應屬性相關聯的 N 維空間中的向量。新觀察到的實例的期望屬性是通過對屬于每個可能分類的實例的相似性度量求和來預測的。然而,盡管基于樣本方法通過模仿物理知識在受限的物理區域內做出了合理的預測,但它不能推廣到先前未知的區域中。基于深度學習的模型則具有 “學習” 的能力,可以從先前未知的數據中預測到物體的屬性。本文重點關注的就是深度學習如何更好的學習直觀物理學。具體的,文獻 [2] 中提出的模型可以從一個單一的圖像映射到一個牛頓假設(Newtonian scenario)狀態。這種映射需要學習微小視覺和上下文線索,以便能夠對正確的牛頓假設、狀態、視點等進行推理。然后可以通過借用與牛頓假設建立的對應關系的信息,對圖像中對象的動力學進行物理預測,從而根據靜止圖像中查詢對象的速度和力方向來預測運動及其原因。文獻 [3] 關注直接從視覺輸入預測物理穩定性的機制。作者沒有選擇顯式的三維表示和物理模擬,而是從數據中學習視覺穩定性預測模型。文獻 [4] 關注了一個真實世界的機器人操作任務:通過戳來將物體移動到目標位置。作者提出了一種基于深度神經網絡的新型方法,通過聯合估計動態的正向模型和逆向模型,直接從圖像中對機器人的交互動態進行建模。逆向模型的目標是提供監督,以構建信息豐富的視覺特征,然后正向模型可以預測這些特征,并反過來為逆向模型規范化特征空間。文獻[5] 設計并實現了一個利用視覺和觸覺反饋對動態場景中物體的運動進行物理預測的系統。其中感知系統采用多模態變分自編碼神經網絡結構,將感知模式映射到一個共享嵌入,用于推斷物理交互過程中物體的穩定靜止形態。
1、深度學習處理不同直觀物理學問題的研究進展
1.1 Newtonian Image Understanding: Unfolding the Dynamics of Objects in Static Images [2]
https://arxiv.org/abs/1511.04048
本文重點研究在靜態圖像中預測物體動態的問題。人類的感知系統具有強大的物理理解能力,甚至能夠對單個圖像進行動力學預測。例如,大多數人都能可靠地預測排球運動的動力學表現(Dynamics),如圖 3 所示。
圖 3. 給定一個靜態圖像,目標是推斷查詢對象的動力學表現(作用在對象上的力以及對象對這些力的預期運動
1.1.1 基本思路
從圖像中估計物理量化指標是一個極具挑戰性的問題。例如,計算機視覺文獻并沒有提供一個可靠的解決方案來從圖像直接估計質量、摩擦力、斜面角度等。因此,本文作者將物理理解問題描述為從圖像到物理抽象的映射,而不是從圖像直接估計物理量。作者遵循與經典力學的相同原理,并使用牛頓假設作為物理抽象,具體場景如圖 4 所示。給定一個靜態圖像,作者的目標是對查詢對象在三維空間中的長期運動進行推理。為此,作者使用一個稱為牛頓假設(圖 4)的中間物理抽象,由游戲引擎渲染。
圖 4. 牛頓假設是根據不同的物理量來定義的:運動方向,力等等。我們使用 12 個假設來描述。圓表示對象,箭頭表示其運動方向
本文使用牛頓神經網絡(Newtonian Neural Network,N^ 3)學習牛頓假設中的一個從單一圖像到狀態的映射。牛頓假設的狀態對應于游戲引擎生成的視頻中的特定時刻,并包含該時刻的一組豐富物理量(力、速度、三維運動)。通過映射到牛頓假設的一個狀態,作者可以借用對應的物理量化指標,并使用它們來預測單個圖像中查詢對象的長期運動趨勢。
在牛頓假設中,從一幅圖像到一種狀態的映射需要解決兩個問題:(a)找出哪個牛頓假設能夠最好的解釋圖像的動力學;(b)在假設中找到與運動中物體狀態相匹配的正確時刻。通過引入上下文和視覺線索,可以解決第一個問題。然而,第二個問題涉及到對微小視覺線索的推理,這種推理對于人類來說都是非常困難的。N^ 3采用數據驅動的方法,利用視覺線索和抽象的運動知識同時學習(a)和(b)。N^ 3利用二維卷積神經網絡(CNN)對圖像進行編碼。為了了解運動,N^ 3使用 3D CNNs 來表示牛頓假設的游戲引擎視頻。通過聯合嵌入,N^ 3學習將視覺線索映射到牛頓假設中的精確狀態。
1.1.2 N^ 3模型分析
作者首先構建了一個視覺牛頓動力學(VIsual Newtonian Dynamics,VIND)數據集,其中包含游戲引擎視頻、自然視頻和牛頓假設對應的靜態圖像。使用游戲引擎構建牛頓假設。游戲引擎將場景配置作為輸入(例如,地平面上方的球),并根據物理學中的運動定律及時模擬它。對于每一個牛頓假設,作者從不同的角度給出了相應的游戲引擎假設。總共獲得 66 個游戲引擎視頻。對于每個游戲引擎視頻,除了存儲 RGB 圖像外,還存儲其深度圖、曲面法線和光流信息。游戲引擎視頻中的每一幀總共有 10 個通道。此外,作者還構建了一組描述運動物體的自然視頻和圖像。目前用于動作或物體識別的數據集不適合于本文的任務,因為它們要么包含了一些超越經典動力學的復雜運動,要么就不顯示任何運動。
作者為每個圖像 / 幀提供三種類型的注釋:(1)至少一種牛頓假設描述的對象的邊界框注釋,(2)視點信息,即游戲引擎視頻的哪個視點最能描述圖像 / 視頻中的運動方向,(3)狀態注釋。對應于牛頓場景(1)的示例游戲引擎視頻如圖 5 所示。
圖 5. 視點注釋。要求注釋者選擇最能描述圖像中對象視圖的游戲引擎視頻(在牛頓假設的 8 個不同視圖中)。游戲引擎視頻中的對象顯示為紅色,其移動方向顯示為黃色。帶有綠色邊框的視頻是選定的視點。
圖 6 給出 N^ 3 的示意圖。N^ 3由兩個平行的卷積神經網絡(CNNs)組成,其中一個用來編碼視覺線索,另一個用來表示牛頓運動。N^ 3的輸入是一個帶有四個通道的靜態圖像(RGBM,其中 M 是對象掩碼通道,通過使用高斯核平滑的邊界框掩碼指定查詢對象的位置)和 66 個牛頓假設視頻,其中每個視頻有 10 幀(從整個視頻中采樣的等距幀),每個幀有 10 個通道(表示 RGB、流、深度和曲面法線)。N^ 3的輸出是一個 66 維向量,其中每個維度表示分配給牛頓假設視點的輸入圖像的置信度。N^ 3通過強制靜態圖像的向量表示和對應于牛頓假設的視頻幀的向量表示之間的相似性來學習映射。狀態預測是通過在牛頓空間中尋找與靜態圖像最相似的幀來實現的。
第一行(編碼視覺線索)類似于文獻 [6] 中介紹的用于圖像分類的標準 CNN 架構。我們將這一行稱為圖像行。圖像行有五個 2D CONV 層(卷積層)和兩個 FC 層(全連接層)。第二行表示牛頓運動的網絡,是受 [7] 啟發的體積卷積神經網絡(Volumetric convolutional neural network)。我們把這一行稱為運動行。運動行有六個 3D CONV 層和一個 FC。運動行的輸入是一批 66 個視頻(對應于游戲引擎渲染的 66 個牛頓假設)。運動行生成 4096x10 的矩陣作為每個視頻的輸出,其中該矩陣中的一列可視為視頻中幀的描述符。為了在輸出中保持相同的幀數,作者消除了運動行中所有 CONV 層在時間維度上的 MaxPooling。這兩行由匹配層連接起來,匹配層使用余弦相似性作為匹配度量。圖像行的輸入是 RGBM 圖像,輸出是 4096 維向量(FC7 層之后的值)。這個向量可以看作是輸入圖像的視覺描述符。匹配層以圖像行的輸出和運動行的輸出作為輸入,計算圖像描述符與該批視頻中所有 10 幀描述符之間的余弦相似度。因此,匹配層的輸出是 66 個向量,每個向量有 10 維。具有最大相似值的維數表示每個牛頓假設的動力學狀態。例如,如果第三維具有最大值,則意味著輸入圖像與游戲引擎視頻的第三幀具有最大相似性,因此其必須具有與相應游戲引擎視頻中的第三幀相同的狀態。在余弦相似層之后附加一個 SoftMax 層,以選取最大相似性作為每個牛頓假設的置信分數。這使得N^ 3能夠在沒有任何狀態級注釋的情況下學習狀態預測。這是N^ 3的一個優勢,它可以通過直接優化牛頓假設的預測來隱式地學習運動狀態。這些置信度分數與來自圖像行的置信度分數線性組合以產生最終分數。
圖 6. N^ 3示意圖
1.1.3 實驗分析
作者使用 Blender 游戲引擎渲染對應于 12 個牛頓假設的游戲引擎視頻。給定一幅圖像和一個查詢對象,作者評估本文方法估計對象運動的能力。表 1 列出了一組與若干基線方法的比較結果。第一個基線稱為直接回歸(Direct Regression),是從圖像到三維空間中軌跡的直接回歸(ground-truth 曲線由 1200 節的 B 樣條曲線表示)。對于這個基線,作者修改了 AlexNet 架構,使每個圖像回歸到其相應的 3D 曲線。表 1 顯示,N^ 3顯著優于這一基線方法。作者假設這主要是由于輸出的維度以及微小視覺線索和物體的三維運動之間復雜的相互作用。
為了進一步探索直接回歸是否可以粗略估計軌跡形狀的問題,作者建立了一個更強大的基線 ----“直接回歸 - 最近(Direct Regression-Nearest)”,使用上述直接回歸基線的輸出來尋找牛頓假設中最相似的 3D 曲線(基于 B 樣條表示之間的標準化歐氏距離)。表 1 顯示,N^ 3也優于這一基線方法。
表 1. 三維物體運動的估計,采用 F - 測度作為評價指標
圖 7 給出了在靜止圖像中估計對象預期運動的定性實驗結果。當N^ 3預測圖像的 3D 曲線時,它也會估計視點。這使我們能夠將 3D 曲線投影回圖像上。圖 7 給出了這些估計運動的示例。例如,N^ 3正確地預測了足球投擲的運動(圖 7(f)),并估計了乒乓球下落的正確運動(圖 7(e))。請注意,N^ 3無法解釋將來可能與場景中其他元素發生的碰撞。例如,圖 7(a)給出足球運動員的預測運動。此圖還顯示了一些失敗的示例。圖 7(h)中的錯誤可能是由于球員與籃球之間的距離過大。當我們將 3D 曲線投影到圖像時,還需要假設到相機的距離,2D 投影曲線的比例可能不一致。
圖 7. 橙色顯示靜態圖像中對象的預期運動。作者可視化了物體的三維運動(紅色球體)及其在圖像上的疊加(左圖),紅框中還顯示了失敗案例,其中紅色和綠色曲線分別表示本文預測結果和真實情況
有趣的是,N^ 3還可以預測查詢對象靜態圖像中合力(Net force)和速度的方向!圖 8 給出了定性示例。例如,N^ 3可以預測保齡球示例中的摩擦力以及籃球示例中的重力。由于地板的法向力抵消了重力,所以施加在最下面一排(左)椅子上的合力為零。
圖 8. 合力方向和物體速度可視化展示。速度以綠色顯示,合力以紅色顯示。相應的牛頓假設顯示在每張圖片的上方
1.2 Visual Stability Prediction and Its Application to Manipulation [3]
https://arxiv.org/abs/1609.04861
1.2.1 基本思路
嬰兒在很小的時候就能夠通過觀察獲得關于物理事件的知識。例如,支撐:一個物體如何穩定地抓住另一個物體;碰撞:一個移動的物體如何與另一個物體相互作用。根據他們的研究,嬰兒或許具有先天能力的通過觀察身體事件的各種結果,能夠逐漸建立起自身身體事件的內部模型。嬰兒先天具備的物理事件的基本知識,例如對支撐現象的理解,可以使其完成對相對復雜的構造結構的操作。這種結構是通過堆疊一個元件或移除一個元件而產生的,同時主要依靠對這種玩具結構中支撐事件的有效了解來保持結構的穩定性。在本文工作中,作者針對這個支撐事件,建立了一個機器學習模型(視覺穩定性分類器)來預測堆疊對象的穩定性。
作者通過在一系列條件下,包括不同數量的木塊、不同的木塊尺寸、平面與多層結構等,綜合生成一組大木塊塔來解決預測穩定性的問題。通過模擬器運行這些配置(僅在訓練時!)以便生成塔是否會倒塌的標簽。此外,作者還應用該方法指導機器人堆疊木塊。為了避免合成圖像和真實場景圖像之間的域偏移,作者提取了合成圖像和捕獲圖像的前景掩模(Foreground mask)。給定一個真實的塊結構,機器人使用訓練在合成數據上的模型(視覺穩定性分類器)來預測可能的候選位置的穩定性結果,然后對可行的位置進行疊加。如圖 9 所示,作者構建了一個試驗臺,Baxter 機器人的任務是在給定的木塊結構上堆疊一個木塊,而不破壞結構的穩定性。
圖 9. 給定一個木塊結構,視覺穩定性分類器預測未來放置的穩定性,然后機器人會在預測的穩定放置中堆疊一個木塊
1.2.2 視覺穩定性預測
圖 10. 學習視覺穩定性方法概述。需要注意的是,物理引擎只在訓練時用于獲取 groung-truth 來訓練深度神經網絡,而在測試時,只給學習模型提供渲染的場景圖像來預測場景的物理穩定性
首先,圖 10 中給出了視覺穩定性方法的整體結構。本文實驗中生成以長方體塊為基本元素的合成數據。在不同的場景中,塊數、塊大小和疊加深度是不同的,我們稱之為場景參數。
a) 塊數量:通過改變塔的大小來影響任務難度,并挑戰塔在人類和機器中的穩定性。顯然,隨著塊數的增加,接觸面和相互作用的數量增多,使問題越來越復雜。因此,我們將具有四個不同塊數的場景設置為{4B,6B , 10B, 14B},即 4 塊、6 塊、10 塊和 14 塊。
b) 疊加深度:當研究目的是從單目輸入判斷穩定性時,作者改變了塔的深度,從單層設置(稱之為 2D)到多層設置(稱之為 3D)。第一層設置僅允許沿圖像平面在所有高度級別上疊加單個塊,而另一層不強制執行此類約束,并且可以在圖像平面中展開。如表 2 所示。
c) 塊大小:本文實驗包括了兩組塊大小設置。在第一種設置中,塔是由大小都為 1 x1 x 3 的塊構成的。第二種設置中引入了不同的塊大小,其中三個維度中的兩個是隨機縮放的,隨機分布滿足 [1-δ, 1+δ] 附近的截斷正態分布(Truncated Normal Distribution)N(1, σ^2)。這兩種設置表示為{Uni, NonUni}。第二種設置中引入了非常微小的視覺線索,整個塔的穩定性取決于不同大小的塊之間的小間隙。這種任務對于人類來說都是非常有難度的。
d) 場景:結合這三個場景參數,作者定義了 16 個不同的場景組。例如,組 10B-2D-Uni 表示使用相同大小的 10 個塊堆疊在單個層中的場景。對于每個場景組,生成 1000 個候選場景,其中每個候選場景都以自底向上的方式用不重疊的幾何約束構造。總共有 16K 個場景。
e) 渲染:本實驗中不使用彩色磚塊,從而使得識別磚塊輪廓和配置的任務更有挑戰性。整個場景的照明固定、攝像機自動調整,從而保證塔位于拍攝圖像的中心。圖像以 800 x 800 的彩色分辨率渲染。
f) 物理引擎:使用 Panda3D 中的 Bullet 完成每個場景在 1000Hz 下 2 秒的物理模擬。在模擬中啟用了表面摩擦和重力。系統記錄時刻 t 內一個場景中的 N 個塊為(p_1, p_2,..., p_N)_t,其中 p_i 為塊 i 的位置。然后將穩定性自動確定為布爾變量:
其中,T 表示模擬的結束時間,Δ用于衡量起始和結束時間之間塊的位移情況,τ為位移閾值,V 表示邏輯或。計算的結果 True 或 False 表示這個場景是 “不穩定” 或者“穩定”。
對于人類來說,不管其解析視覺輸入的實際內在機制如何,很明顯存在一個涉及視覺輸入 I 到穩定性預測 P 的映射 f:
其中,* 表示其它可能的信息。
在本文工作中,感興趣的是 f 到視覺輸入的映射,并直接預測物理穩定性。作者使用了深度卷積神經網絡,因為它在圖像分類任務中的應用效果非常好。這種網絡通過重新訓練或微調自適應,能夠適應廣泛的分類和預測任務。因此,作者認為它是研究視覺預測這一具有挑戰性的任務的適當方法。
作者使用 LeNet(一個相對較小的數字識別網絡)、AlexNet(一個較大的網絡)和 VGG-Net(一個比 AlexNet 更大的網絡)對生成的數據子集進行了測試。作者發現在測試過程中 VGG 網絡始終優于其他兩個,因此本文最終使用的深度學習方法是 VGG,且所有的實驗中都使用了 Caffe 框架。
表 2. 渲染場景中的場景參數概述。有 3 組場景參數,包括塊數、疊加深度和塊大小
為了評估任務的可行性,作者首先在具有相同場景參數的場景上進行訓練和測試,稱為組內實驗(Intra-Group Experiment),實驗結果見表 3。在這組實驗中,固定疊加深度且保持場景中所有塊的大小相同,但改變場景中塊的數量,以觀察該參數對圖像訓練模型預測率的影響。在不同的塊大小和堆疊深度條件下,隨著場景中塊數的增加,可以觀察到穩定性能在持續下降。場景中的塊越多,通常導致場景結構塔的高度越高,因此感知難度就越大。此外,作者還探討了相同大小和不同大小的塊如何影響圖像訓練模型的預測率,當從 2D 堆疊移動到 3D 堆疊時,穩定性能會下降。塊大小帶來的額外變化確實加大了穩定性任務的難度。最后,作者研究了堆疊深度對預測率的影響。隨著堆疊深度的增加,對場景結構的感知越來越困難,場景的某些部分可能被其他部分遮擋或部分遮擋。對于簡單場景,當從 2D 堆疊移動到 3D 時,預測精度提高,而對于復雜場景則是相反的。
表 3. 組內實驗結果
為了進一步了解模型如何在具有不同復雜度的場景之間變化,作者根據塊數將場景組分為兩大組,進行組間實驗(Cross-Group Experiment),包括一個具有 4 和 6 個塊的簡單場景組和一個具有 10 和 14 個塊的復雜場景組。實驗結果見表 4。作者對簡單場景進行訓練,對復雜場景進行預測,最終預測率為 69.9%,明顯優于 50% 的隨機猜測。作者認為這是因為學習的視覺特征可以在不同的場景中傳遞。此外,在復雜場景中訓練并對簡單場景進行預測時,模型的性能顯著提高。作者分析這可能是由于模型能夠從復雜場景中學習到更豐富和更好的泛化特征。
表 4. 組間實驗結果
1.2.3 操作控制(Manipulation)
進一步,作者探索合成數據訓練模型是否以及如何用于實際應用,特別是用于機器人操作控制中。因此,作者建立了一個如圖 9 所示的試驗臺,Baxter 機器人的任務是在給定的木塊結構上堆疊一個木塊,而不破壞結構的穩定性。該實驗系統的完整結果如圖 12。實驗中使用 Kapla 塊作為基本單元,并將 6 個塊粘貼到一個較大的塊中,如圖 13a 所示。為了簡化任務,作者對自由式堆疊進行了調整:
與上一節中的 2D 情況一樣,將給定的塊體結構限制為單層。在最后的測試中,作者報告了 6 個場景的結果,如表 5 所示。
將放在給定結構頂部的塊限制為兩個規范配置{vertical,horizongtal},如圖 13b 所示,并假設在放置之前是被機器人握在手中的。
將塊約束為放置在給定結構的最頂層水平面(堆疊面)上。
校準結構深度(與機器人的垂直距離),這樣只需要確定相對于堆疊的塔表面的水平和垂直位移。
圖 12. 控制系統概覽
圖 13. 實驗中用到的積木
為了應對真實世界物體圖片與合成數據的不同,作者在合成數據的二值前景模板上訓練視覺穩定性模型,并在測試時對模板進行處理。這樣,就大大降低了真實世界中彩色圖片的影響。在測試時,首先為空場景捕獲背景圖像。然后,對于表 5 中所示的每個測試場景捕獲圖像并通過背景減法將其轉換為前景遮罩。檢測最上面的水平邊界作為堆疊表面用于生成候選放置:將該表面均勻劃分為 9 個水平候選和 5 個垂直候選,因此總共有 84 個候選。整個過程如圖 14 所示。然后,將這些候選對象放入視覺穩定性模型中進行穩定性預測。每個生成的候選對象的實際穩定性都手動測試并記錄為 ground-truth。最終的識別結果如表 5 所示。由該表中實驗結果可知,使用合成數據訓練的模型能夠在現實世界中以 78.6% 的總體準確率預測不同的候選對象。
圖 14. 為給定場景生成候選放置圖像的過程
表 5. 真實世界測試的結果。“Pred.”是預測精度。“Mani.”是操縱成功率,包括每個場景的成功放置 / 所有可能的穩定放置計數。“H/V”指水平 / 垂直放置
1.3 Learning to Poke by Poking: Experiential Learning of Intuitive Physics [4]
https://arxiv.org/abs/1606.07419
1.3.1 基本思路
人類具備對工具進行泛化的能力:我們可以毫不費力地使用從未見過的物體。例如,如果沒有錘子,人們可能會用一塊石頭或螺絲刀的背面來敲打釘子。是什么使人類能夠輕松地完成這些任務呢?一種可能性是,人類擁有一個內在的物理模型(直觀物理),使他們能夠對物體的物理特性進行推理,并預測其在外力作用下的動態。這樣的模型可以用來把一個給定的任務轉換成一個搜索問題,其方式類似于在國際象棋或 tic-tac-toe 游戲中通過搜索游戲樹來規劃移動路徑。由于搜索算法與任務語義無關,因此可以使用相同的機制來確定不同任務(可能是新任務)的解決方案。
小嬰兒在成長的過程中總是會以一種看似隨機的方式玩東西,他們并沒有明確的“目標”。關于嬰兒這種行為的一種假設是嬰兒將這種經驗提煉成了直觀物理模型,預測他們的行為如何影響物體的運動。一旦學會了,他們就可以利用這些模型規劃行動,以應對新的出現在生活中的物體。受這一假設的啟發,本文研究了機器人是否也可以利用自己的經驗來學習一個直觀的有效物理模型。在圖 15 所示的任務場景中,Baxter 機器人通過隨機戳(Poke)放在它前面桌上的物體來與它們互動。機器人在 Poke 之前和之后記錄視覺狀態,以便學習其動作與由物體運動引起的視覺狀態變化之間的映射。到目前為止,本文的機器人已經與物體進行了 400 多個小時的互動,并在這個過程中收集了超過 10 萬個不同物體上的 Poke。機器人配備了 Kinect 攝像頭和一個夾子,用來戳放在它前面桌子上的物體。在給定的時間內,機器人從桌上 16 個不同的目標對象中選擇 1-3 個對象。機器人的坐標系為:X 軸和 Y 軸分別代表水平軸和垂直軸,Z 軸則指向遠離機器人的方向。機器人通過用手指沿著 XZ 平面從桌子上移動一個固定的高度來戳物體。
為了收集交互數據的樣本,機器人首先在其視野中選擇一個隨機的目標點來戳。隨機戳的一個問題是,大多數戳是在自由空間中執行的,這嚴重減慢了有效交互數據的收集過程。為了快速收集數據,作者使用 Kinect 深度相機的點云只選擇位于除桌子以外的任何對象上的點。點云信息僅在數據采集階段使用,在測試時,本文的系統只需要使用 RGB 圖像數據。在對象中隨機確定一個點 poke(p),機器人隨機采樣 poke 的方向 (θ) 和長度(l)。
這個機器人可以無需任何人工干預的全天候自主運行。有時當物體被戳到時,它們會按預期移動,但有時由于機器人手指和物體之間的非線性交互作用,它們會以意外的方式移動,如圖 16 所示。所以模型必須能夠處理這種非線性交互。項目早期的少量數據是在一張背景為綠色的桌子上收集的,但實際上絕大部分數據是在一個有墻的木制區域中收集的,主要目的是防止物體墜落。本文的所有結果都來自于從木制區域收集的數據。
圖 15. 機器人通過隨機戳來與物體互動。機器人戳物體并記錄戳前(左圖)和戳后(右圖)的視覺狀態。利用前圖像、后圖像和應用 poke 的三元組訓練神經網絡(中間圖),學習動作與視覺狀態變化之間的映射關系
圖 16. 這些圖像描繪了機器人將瓶子從指示虛線移開的過程。在戳的中間,物體會翻轉,最后朝著錯誤的方向移動。這種情況很常見,因為現實世界中的對象具有復雜的幾何和材質特性
1.3.2 模型分析
機器人應該從經驗中學習什么樣的模型?一種可能性是建立一個模型,根據當前的視覺狀態和施加的力來預測下一個視覺狀態(即正向動力學模型)。本文提出了一個聯合訓練正向和反向動力學模型。正向模型根據當前狀態和動作預測下一個狀態,反向模型根據初始狀態和目標狀態預測動作。在聯合訓練中,反向模型目標提供監督,將圖像像素轉化為抽象的特征空間,然后由正向模型預測。反向模型減輕了正向模型在像素空間中進行預測的需要,而正向模型反過來又使反向模型的特征空間正則化。
使用公式(1)和公式(2)分別定義正向、反向模型:
其中,x_t, u_t 分別表示應用于時間步長 t 的世界狀態和動作,^x_t+1, ^u_t+1 是預測的狀態和動作,W_fwd 和 W_inv 是用于構建正向和反向模型的函數 F 和 G 的參數。給定初始狀態和目標狀態,反向模型給出了映射到直接能夠實現目標狀態所需的操作(如果可行的話)。然而,多種可能的行為可能將當前的世界狀態從一種視覺狀態轉換為另一種視覺狀態。例如,如果 agent 移動或 agent 使用其手臂移動對象,則對象可能出現在機器人視野的某個部分。行動空間中的這種多模態使得學習變得非常困難。另一方面,給定 x_t 和 u_t,存在下一狀態 x_t+1,該狀態對于動力學噪聲是唯一的。這表明正向模型可能更容易學習。
然而,在圖像空間學習正向模型是很困難的,因為預測未來幀中每個像素的值是非常困難的。在大多數場景中,我們對預測具體的像素不感興趣,而是希望能夠預測更抽象事件的發生,例如對象運動、對象姿勢的變化等。使用正向模型的第二個問題是,推斷最優行為不可避免地會導致找到受局部最優約束的非凸問題的解。而反向模型就沒有這個缺點,因為它直接輸出所需的動作。這些分析表明,反向模型和正向模型具有互補的優勢,因此有必要研究反向模型和正向動力學的聯合模型。
本文使用的學習正向和反向動力學的聯合深度神經網絡如圖 17 所示。
圖 17. 聯合深度神經網絡示例
訓練樣本包括一組前圖像 (I_t)、后圖像(I_t+1) 和機器人動作 (u_t)。在隨后的時間步長(I_t,I_t+1) 內將樣本輸入五個卷積層以得到潛在特征表示 (x_t, x_t+1),這五個卷積層與 AlexNet 的前五層結構相同。為了建立反向模型,串聯 x_t,x_t+1 并通過全連接層來有條件地分別預測戳的位置(p_t)、角度(θ_t) 和長度 (l_t)。為了模擬多模態戳分布,將戳的位置、角度和長度分別離散化為 20x 20 的網格、36 個 bins 和 11 個 bins。戳長度的第 11 個 bin 用于表示沒有戳(no poke)。為了建立正向模型,將正向圖像的特征表示(x_t) 和動作(u_t,未離散化的實值向量)傳遞到一個全連接層序列中,該序列預測下一幅圖像 (x_t+1) 的特征表示。優化下式中的損失以完成訓練:
其中,L_inv 為真實和預測的戳位置、角度和長度的交叉熵損失和。L_fwd 為預測和 ground-truth 之間的 L1 損失。W 為神經網絡的權重。
測試該模型的一種方法是向機器人提供初始圖像和目標圖像,并要求它進行戳的動作將物體移動到目標圖像顯示的位置中。當初始圖像和目標圖像對的視覺統計與訓練集中的前后圖像相似時,機器人就成功地完成了動作。如果機器人能夠將物體移動到目標位置,而目標位置與物體在一次戳之前和之后的位置相比相距更遠,作者認為這表明該模型可能了解了物體在被戳時如何移動的基本物理原理。如果機器人能夠在多個干擾物存在的情況下推動具有幾何形狀和紋理復雜的物體,則說明模型的能力更強。如果初始圖像和目標圖像中的對象之間的距離超過了單個戳的動作可以推的最大距離,則需要模型輸出一系列戳。作者使用貪婪計劃方法(見圖 18(a))來輸出戳序列。首先,描述初始狀態和目標狀態的圖像通過該模型來預測戳,由機器人執行。然后,將描述當前世界狀態的圖像(即當前圖像)和目標圖像再次輸入到模型中以輸出戳。重復此過程,當機器人預測無戳或達到 10 個戳時結束。
在所有的實驗中,初始圖像和目標圖像只有一個物體的位置是不同的。將機器人停止后最終圖像中物體的位置和姿態與目標圖像比較后進行定量評價。通過計算兩張圖像中物體位置之間的歐氏距離來得到位置誤差。在初始狀態和目標狀態下,為了考慮不同的目標距離,作者使用相對位置誤差代替絕對位置誤差。姿態誤差則定義為最終圖像和目標圖像中物體長軸之間的角度(以度為單位)(見圖 18(c))。
圖 18. (a) 貪婪規劃算子用于輸出一系列戳,以將對象從初始配置置換到目標圖像。(b) blob 模型首先檢測對象在當前圖像和目標圖像中的位置。根據物體的位置,計算出戳的位置和角度,然后由機器人執行。利用得到的下一幀圖像和目標圖像來計算再下一幀圖像,并迭代地重復這個過程。(c) 模型將物體戳到正確姿勢的誤差度量為最終圖像和目標圖像中物體長軸之間的夾角
本文作者選擇 blob 模型作為基線對比模型(圖 18(b))。該模型首先利用基于模板的目標檢測器估計目標在當前圖像和目標圖像中的位置。然后,它使用這兩者之間的向量差來計算機器人執行的戳的位置、角度和長度。以類似于對學習模型進行貪婪規劃的方式,迭代地重復此過程,直到對象通過預定義的閾值更接近目標圖像中的所需位置或達到最大戳數。
1.3.3 實驗分析
本文實驗中機器人的任務是將初始圖像中的物體移動到目標圖像描述的形狀中(見圖 19)。圖 19 中的三行顯示了當要求機器人移動訓練集中的對象(Nutella 瓶)、幾何結構與訓練集中的對象不同的對象(紅杯子)以及當任務是繞障礙物移動對象時的性能。這些例子能夠表征機器人的性能,可以看出,機器人能夠成功地將訓練集中存在的對象以及復雜的新的幾何結構和紋理的對象戳入目標位置,這些目標位置明顯比訓練集中使用的一對前、后圖像更遠。更多的例子可以在項目網站上找到(http://ashvin.me/pokebot-website/)。圖 19 中的第 2 行還顯示,在當前圖像和目標圖像中占據相同位置的干預物體的存在并不會影響機器人的性能。這些結果表明,本文模型允許機器人執行超出訓練集的泛化任務(即小距離戳物體)。圖 19 中的第 3 行給出了一個機器人無法將物體推過障礙物(黃色物體)的例子。機器人貪婪地行動,最后的結果是一起推障礙物和物體。貪婪規劃的另一個副作用是使得物體在初始位置和目標位置之間的運動軌跡呈現鋸齒形而不是直線軌跡。
圖 19. 機器人能夠成功地將訓練集中的物體(第 1 行;Nutella 瓶)和未知幾何體物體(第 2 行;紅杯)移動到目標位置,這些目標位置比訓練集中使用的一對前、后圖像要遠得多。機器人無法推動物體繞過障礙物(第 3 行;貪婪規劃限制)
機器人究竟是怎么做到的呢?作者分析,一種可能是機器人忽略了物體的幾何結構,只推斷出物體在初始圖像和目標圖像中的位置,并使用物體位置之間的差向量來推斷要執行的動作。當然,這并不能證明模型已經學會目標檢測了。不過作者認為其所學習的特征空間的最近鄰可視化結果能夠表明它對于目標位置是敏感的。不同的物體有不同的幾何形狀,所以為了能夠以相同的方式移動它們,就需要在不同的地方戳它們。例如,對于 Nutella 瓶子來說,不需要旋轉瓶子,只需要沿著朝向其質心的方向在側面戳瓶子。對于錘子來說,移動它的方法則是在錘頭與手柄接觸的地方戳。
與將對象推到所需位置相比,將對象推到所需姿勢更困難,需要更詳細地了解對象幾何特征。為了測試學習到的模型是否能夠表征與對象幾何特征有關的信息,作者將其性能與忽略對象幾何特征的基線 Blob 模型(見圖 18(b))進行了比較。在這個對比實驗中,機器人的任務是只戳一次就把物體推到附近的目標。圖 20(a)中的結果表明,反向模型和聯合模型都優于 blob 模型。這表明除了能夠表征對象位置的信息外,本文的模型還能夠表征對象幾何特征相關的信息。
在二維仿真環境中,作者還檢驗了正向模型是否正則化了反向模型學習到的特征空間。在二維仿真環境中,機器人使用較小的力量戳一個紅色矩形物體來與之交互。允許矩形自由平移和旋轉(圖 20(c))。圖 20(c)顯示,當可用的訓練數據較少(10K、20K 實例)時,聯合模型的性能優于反向模型,并且能夠以較少的步驟(即較少的動作)接近目標狀態。這表明,正向模型確實對反向模型的特征空間進行了正則化處理,從而使其具有更好地推廣和泛化性能。然而,當訓練實例的數量增加到 100K 時,兩個模型性能相同。作者認為這是由于使用更多數據的訓練通常直接就能夠導致較好的泛化性能,此時反向模型不再依賴于正向模型的正則化處理。
圖 20. (a) 反向模型和聯合模型在將物體推向所需姿勢時比 blob 模型更精確;(b) 當機器人在訓練集使用的前后圖像中按明顯大于物體距離的距離推動物體時,聯合模型的性能優于純反向模型;(c)當訓練樣本數較少(10K、20K)時,聯合模型的性能優于反向模型,且與較大的數據量(100K)相當
1.4 Learning Intuitive Physics with Multimodal Generative Models [5]
https://arxiv.org/abs/2101.04454
1.4.1 基本思路
人類如何通過對物體初始狀態的視覺和觸覺測量來預測其未來的運動?如果一個以前從來沒見過的物體落入手中,我們可以推斷出這個物體的類別,猜測它的一些物理性質,之后判斷它是否會安全地停在我們的手掌中,或者我們是否需要調整對這個物體的抓握來保持與其接觸。視覺(Vision)允許人類快速索引來捕捉物體的整體特性,而接觸點的觸覺信號可以使人對平衡、接觸力和滑動進行直接的物理推理。這些信號的組合使得人類能夠預測對象的運動,即通過觸覺和視覺感知物體的初始狀態,預測物體被動物理動力學(Passive Physical Dynamics)的最終穩定結果。
前期研究結果表明,由于相互作用表面的未知摩擦、未知幾何特征以及不確定的壓力分布等因素,預測運動物體的運動軌跡非常困難。本文重點研究學習一個預測器,訓練它捕捉運動軌跡中最有用和最穩定的元素。如圖 21 所示,當預測對瓶子施加推力的結果時,預測器應該能夠考慮這個動作最主要的后果:瓶子會翻倒還是會向前移動?為了研究這個問題,作者提出了一種新的人工感知方法,它由硬件和軟件兩部分組成,可以測量和預測物體落在物體表面的最終靜止形態。作者設計了一種能夠同時捕捉視覺圖像和提供觸覺測量的新型傳感器 ---- 穿透皮膚(See-Through-your-Skin,STS)傳感器,同時使用一個多模態感知系統的啟發多模態變分自動編碼器(Multimodal variational autoencoder,MVAE)解釋 STS 的數據。
圖 21. 預測物理相互作用的結果。給定瓶子上的外部擾動,我們如何預測瓶子是否會傾倒或平移?
1.4.2 模型介紹
首先介紹 STS 傳感器,它能夠渲染接觸幾何體和外部世界的雙流高分辨率圖像。如圖 22 所示,STS 的關鍵特征為:
多模態感知(Multimodal Perception)。通過調節 STS 傳感器的內部照明條件,可以控制傳感器反射涂料涂層的透明度,從而允許傳感器提供有關接觸物體的視覺和觸覺反饋。
高分辨率傳感(High-Resolution Sensing)。視覺和觸覺信號都以 1640 x 1232 的高分辨率圖像給出。使用 Odeseven 的 Raspberry Pi 可變焦距相機模塊,提供 160 度的視野。這會產生兩個具有相同視角、參考系和分辨率的感知信號。
圖 22. STS 傳感器的可視化多模態輸出。使用受控的內部照明,傳感器的表面可以變得透明,如左上角所示,允許相機觀察外部世界。在左下圖中,傳感器通過保持傳感器內部相對于外部明亮來提供觸覺特征
STS 視覺觸覺傳感器由柔順薄膜、內部照明源、反射漆層和攝像頭組成。當物體被壓在傳感器上時,傳感器內的攝像機通過 “皮膚” 捕捉視圖以及柔順薄膜的變形,并產生編碼觸覺信息的圖像,例如接觸幾何結構、作用力和粘滑行為。作者使用了一種透明可控的薄膜,允許傳感器提供物理交互的觸覺信息和傳感器外部世界的視覺信息。作者在 PyBullet 環境中為 STS 傳感器開發了一個可視模擬器,該模擬器根據接觸力和幾何形狀重建高分辨率觸覺特征。利用模擬器快速生成動態場景中對象交互的大型可視化數據集,以驗證感知模型的性能。模擬器通過陰影方程映射碰撞物體的幾何信息:
其中,I(x,y)表示圖像強度,z=f(x,y)為傳感器表面的高度圖,R 是模擬環境光照和表面反射率的反射函數。使用 Phong 反射模型實現反射函數 R,該模型將每個通道的照明分為環境光、漫反射光和鏡面反射光三個主要組件:
其中,^L_m 是從曲面點到光源 m 的方向向量,^N 是曲面法線,^R_m 為反射向量,
其中,^V 為指向攝像機的方向向量。
本文提出了一個生成性的多模態感知系統,它將視覺、觸覺和 3D 姿勢(如果可用)反饋集成在一個統一的框架內。作者利用多模態變分自動編碼器(Multimodal Variational Autoencoders,MVAE)來學習一個能夠編碼所有模態的共享潛在表示。作者進一步證明,這個嵌入空間可以編碼有關物體的關鍵信息,如形狀、顏色和相互作用力,這是對直觀物理進行推斷所必需的。動態交互的預測結果可以表示為一個自監督問題(Self-supervision problem),在給定框架下生成目標視覺和觸覺圖像。本文目標是學習一個生成器,它將當前觀測值映射到靜止狀態的預測配置。作者認為,MVAE 結構可以用來預測多模態運動軌跡中最穩定和最有用的元素。
【變分自動編碼器(Variational Autoencoders)】
生成潛在變量模型學習數據的聯合分布和不可觀測的表示:
其中,p_θ(z)和 p_θ(x|z)分別表示先驗分布和條件分布。目標是使邊際可能性最大化:
優化的成本目標為證據下限(Evidence lower bound,ELBO):
其中,第一項表示重建損失,重建損失測量給定潛在變量的重建數據可能性的期望。第二項為近似后驗值和真實后驗值之間的 Kullback-Leibler 散度,在式中作用為正則化項。
【多模變分自動編碼器(Multimodal Variational Autoencoders)】
VAE 使用推理網絡將觀測值映射到潛在空間,然后使用解碼器將潛在變量映射回觀測空間。雖然這種方法在恒定的觀測空間中是可行的,但在多模態情況下卻比較困難,這是由于觀測空間的尺寸隨著模態的可用性而變化。例如,觸覺信息只有在與傳感器接觸時才可用。對于這種數據可用性上具有可變性的多模態問題,需要為每個模態子集訓練一個推理網絡 q(z|X),共產生 2^N 個組合。為了應對這個組合爆炸的問題,本文引入專家乘積模型(Product of Experts,PoE)通過計算每個模態的個體后驗概率的乘積來學習不同模態的近似聯合后驗概率。
多模態生成建模學習所有模態的聯合分布為:
其中,x_i 表示與模態 i 相關的觀測值,N 為模態總數,z 為共享的潛在空間。假設模態之間存在條件獨立性,將聯合后驗分布改寫為:
使用模態 i 的推理網絡替換上式中的 p(z|x_i),可得:
即 PoE。MVAE 的一個重要優點是,與其他多模態生成模型不同,它可以有效地擴展到多種模態,因為它只需要訓練 N 個推理模型,而不是 2^N 個多模態推理網絡。
【用 MVAEs 學習直觀物理】
作者在網絡結構中引入了一個時滯元素(Time-lag element)以訓練變分自動編碼器,其中,將解碼器的輸出設置為預測未來的幀。引入 ELBO 損失:
其中,t 和 T 分別表示輸入和輸出時間實例。
圖 23 給出了動力學模型學習框架,其中視覺、觸覺和 3D 姿勢融合在一起,通過 PoE(product of expert)連接的三個單峰編碼器 - 解碼器學習共享的嵌入空間。為了訓練模型損耗,作者通過列舉模態 M={visual, tactile, pose}的子集來計算 ELBO 損耗:
其中,P(M)為模態集 M 的功率集。在動力學模型有輸入的情況下(例如,第三個模擬場景中的力擾動),將輸入條件 c 對 ELBO 損失的條件依賴性概括為:
圖 23. 多模態動力學建模。在一個統一的多模態變分自動編碼器框架內集成視覺、觸覺和 3D 姿態反饋的生成感知系統。網絡獲取當前對象配置并預測其靜止配置
1.4.3 實驗分析
作者使用前面描述的 PyBullet 模擬器收集模擬數據集,真實數據集則是使用 STS 傳感器的原型收集的。
【模擬數據集】
本文考慮三個模擬的物理場景,如圖 24 所示,涉及從 3D ShapeNet 數據集提取的八個對象類別(bottle, camera, webcam, computer mouse, scissors, fork, spoon, watch)。具體的任務如下:
平面上自由下落的物體。這個實驗在 STS 傳感器上釋放具有隨機初始姿態的物體,在到達靜止狀態之前,它們與傳感器發生多次碰撞。作者收集了總共 1700 個軌跡,包括 100k 圖像。
從斜面上滑下來的物體。這個實驗將具有隨機初始姿勢的物體放置在一個傾斜的表面上,在那里它們要么由于摩擦而粘住不動,要么向下滑動。向下滑動時,對象可能會滾動,此時最終狀態的配置與初始狀態差別非常大。作者共收集 2400 個軌跡,包括 145k 圖像。
穩定的靜止姿勢中受到干擾的物體。在這種情況下,考慮一個物體最初穩定地停留在傳感器上,它被傳感器隨機采樣的快速橫向加速度從平衡點擾動。這個實驗只考慮瓶子,因為它們具有拉長的形狀和不穩定的形狀,在不同方向或受力大小的情況下會出現不同的實驗結果。由于結果的多樣性,這項任務比其他兩項任務要復雜得多。作者總共收集了 2500 條軌跡,包括 150k 圖像。
圖 24. 三個動態模擬場景的模擬示例片段。最上面的行顯示 3D 對象視圖,而中間和底部行分別顯示 STS 傳感器捕獲的視覺和觸覺測量結果
【真實數據集】
真實數據集是使用 STS 傳感器手動收集的一個小的數據集。作者使用一個小型電子設備(GoPro)從 500 個軌跡中收集了 2000 張圖像。之所以選擇這個物體,是因為它的體積小(小到可以裝在 15cm x 15cm 的傳感器原型上)和質量大(重到可以在傳感器上留下有意義的觸覺特征)。每個軌跡都包括通過快速打開 / 關閉傳感器內部燈光獲得的初始和最終視覺、觸覺圖像。如圖 25 所示,在與傳感器接觸的同時,將對象從不穩定的初始位置釋放,一旦對象靜止則確定事件結束。
圖 25. 真實世界的數據收集方法,從不穩定的初始狀態釋放 GoPro 相機
圖 26 和 27 給出了模擬數據集的多模態預測。作者示出了 MVAE 預測物體靜止形態的原始視覺和觸覺測量值的能力,其預測值與 ground-truth 標簽非常吻合。圖 26(a)顯示 MVAE 模型處理缺失模態的能力,例如觸覺信息在輸入中缺失不可用。該模型學習準確預測物體從傳感器表面墜落的情況,產生了空輸出圖像。圖 27 中的結果表明,該模型通過正確預測物體運動的結果(即傾倒或墜落),成功地整合了有關作用力的信息。
圖 26. 模擬數據集的三個場景中多模態預測。除了 STS 傳感器的視覺和觸覺測量之外,該模型還預測了最終的靜止狀態。最下面一行比較預測的姿態(實線坐標)和 ground-truth(虛線坐標)
圖 27. MVAE 與單模 VAE 視覺和觸覺預測的定性比較
圖 28 展示了該模型通過視覺和觸覺圖像預測靜止物體形態的能力。MVAE 與單模 VAE 的視覺預測定性結果表明,MVAE 模型利用觸覺模式能夠對靜止形態進行更準確的推理。
圖 28. 真實數據集中 MVAE 與單模 VAE 視覺預測的定性比較
2、文章小結
這篇文章關注了深度學習如何學習直觀物理學的問題。我們希望機器人也能夠像人類一樣根據所處的物理環境進行規劃并行動。深度學習在整個過程中賦予了機器人 “學習” 的能力,因此,與經典的啟發式方法、概率模擬模型相比,深度學習方法的 “學習” 能力使其能夠學習并學會推斷出物理屬性。本文介紹了四個適用于不同場景的深度學習模型,包括 N^3 牛頓推理模型、VGG、聯合訓練正向和反向動力學模型、多模態變分自編碼神經網絡。這些模型在論文給出的實驗中都表現不錯,不過真實世界中的物理環境、物體運動方式、接觸方式等都是非常復雜的,能夠讓深度學習方法真正獲得類似于人類的應對物理環境的能力,還有待漫長的持續的深入研究。
本文參考引用的文獻:
[1] Kubricht J R , Holyoak K J , Lu H . Intuitive Physics: Current Research and Controversies[J]. Trends in Cognitive Sciences, 2017, 21(10). http://philpapers.org/rec/KUBIPC
[2] Mottaghi R , Bagherinezhad H , Rastegari M , et al. Newtonian Image Understanding: Unfolding the Dynamics of Objects in Static Images[J]. 2015.,http://de.arxiv.org/pdf/1511.04048
[3] Li W , Leonardis, Ale?, Fritz M . Visual Stability Prediction and Its Application to Manipulation[J]. 2016.http://arxiv.org/abs/1609.04861
[4] P Agrawal,A Nair,P Abbeel,J Malik,S Levine, Learning to Poke by Poking: Experiential Learning of Intuitive Physics,http://arxiv.org/abs/1606.07419
[5] Sahand Rezaei-Shoshtari,Francois Robert Hogan,Michael Jenkin,David Meger,Gregory Dudek, Learning Intuitive Physics with Multimodal Generative Models, https://www.researchgate.net/publication/348426682_Learning_Intuitive_Physics_with_Multimodal_Generative_Models
[6] A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012
[7] D. Tran, L. Bourdev, R. Fergus, L. Torresani, and M. Paluri. Learning spatiotemporal features with 3d convolutional networks. In ICCV, 2015
- 免責聲明
- 本文所包含的觀點僅代表作者個人看法,不代表新火種的觀點。在新火種上獲取的所有信息均不應被視為投資建議。新火種對本文可能提及或鏈接的任何項目不表示認可。 交易和投資涉及高風險,讀者在采取與本文內容相關的任何行動之前,請務必進行充分的盡職調查。最終的決策應該基于您自己的獨立判斷。新火種不對因依賴本文觀點而產生的任何金錢損失負任何責任。





 新火種
2023-10-28
新火種
2023-10-28 






















































