更多內容：AI秘籍合集

Hi,你好。我是茶桁。

之前的課程中，我們學習了兩個最重要的回歸方法，一個線性回歸，一個邏輯回歸。也講解了為什么學習機器學習要從邏輯回歸和線性回歸講起。因為我們在解決問題的時候，有限選擇簡單的假設，越復雜的模型出錯的概率也就越高。

本節課中，我們要繼續我們未完成的內容。

還記得，咱們上一節課中最后所說的嗎？在完成了基本回歸之后，該如何去判斷一個模型的好壞，以及如何調整和優化。

好，我們開始本節課程。

PICKLE

本節課中，會重點的給大家做一件事，叫「評測指標」。

在這之前，我們發現了一個麻煩事。就是我們現在需要去觀測我們的分類結果，我們不得不再去執行一遍我們之前的訓練程序，拿到最后的分類結果：

 RM:6.38, LSTAT:24.08, EXPENSIVE:0, Predicated:0 ... RM:6.319, LSTAT:11.1, EXPENSIVE:1, Predicated:0

這很麻煩，訓練結果每次要使用的時候都需要運行一次，這樣非常的麻煩。現在我想要把這個model不要每一次都訓練一下,而是要把它做一個保存，下次用的時候不需要從頭到尾再訓練一次。

現在現在，可以給他做一個persistence，做一個留存。現在就是要做這么一件事情。

 import pickle  with open('logistic_regression.model', 'wb') as f:     pickle.dump(model, f)  with open('w.model', 'wb') as f:     pickle.dump(w, f)  with open('b.model', 'wb') as f:     pickle.dump(b, f)  print('pickle finished')  --- pickle finished

并且最后我得到了三個文件，分別是logistic_regression.model, w.model以及b.model。

現在就可以把訓練完成的model做保存了。之后我們用Pytorch, tenserflow之類的做，它都有這樣的功能。

到這一步之后，我們上一節上所寫的代碼就可以暫時不用了。不過為了整個代碼的完整性，我仍然將其又在本節課的10.ipynb內些了一遍。

那么，我們要用的時候怎么辦呢？如果要用這個對象的時候，將我們之前對文件操作的代碼拿過來，然后將其中的wb參數改成rb，然后再將二進制文件讀取一遍：

 with open('logistic_regression.model', 'rb') as f:     model_r = pickle.load(f)  with open('w.model', 'rb') as f:     w_r = pickle.load(f)  with open('b.model', 'rb') as f:     b_r = pickle.load(f)  print('pickle read finished')

rb的意思是read binary，也就是讀取二進制文件。然后，為了在測試的時候避免混亂，讓我接下來所使用的文件使用的是我重新讀取的模型而不是之前訓練時生成的的，我將重新讀取的這幾個文件命名為model_r，w_r,b_r。

那再之后，雖然不用重新訓練了，但是數據還是要讀取一遍的，并且，按照訓練數據的規則重新整理好, 都完善了之后，就可以開搞進行分類了。

 import pandas as pd from sklearn.datasets import fetch_openml  dataset = fetch_openml(name='boston', version=1, as_frame=True, return_X_y=False, parser='pandas')  data = dataset['data'] target = dataset['target']  dataframe = pd.DataFrame(data)  rm = dataframe['RM'] lstat = dataframe['LSTAT'] dataframe['price'] = dataset['target']  greater_then_most = np.percentile(dataframe['price'], 66) dataframe['expensive'] = dataframe['price'].apply(lambda p: int(p > greater_then_most))   expensive = dataframe['expensive'] random_test_indices = np.random.choice(range(len(rm)), size=100) decision_boundary = 0.5  for i in random_test_indices:     x1, x2, y = rm[i], lstat[i], expensive[i]     predicate = model_r(np.array([x1, x2]), w_r, b_r)     predicate_label = int(predicate > decision_boundary)      print('RM:{}, LSTAT:{}, EXPENSIVE:{}, Predicated:{}'.format(x1, x2, y, predicate_label))

評測指標

好，解決了模型的重復使用之后，我們再回到課程中繼續。

很多人在學習過程中，會覺得「評測指標」是一個沒有那么有趣的事情。比方說，咱們學模型，學算法，就可以去寫程序，可以運行，寫出來的時候會感覺還蠻酷的。但是評測指標呢，很多同學就覺得不是那么有趣。

其實，我想告訴大家，評測指標是一個非常重要的東西。好比完成任何一個任務，不管你現在是完成普通的編程任務，還是要完成一個公司的市場行為、運營行為。一般來說，越復雜的任務，只要把評價指標，評價方式做對，這個任務基本上就已經完成了一半了。

對于我們來說，工作的時候要知道，對于一個機器學習任務，能找到正確的評測指標，這個機器學習任務就已經成功一半了。

首先，來看一個問題：Losses持續下降，到底是意味著什么呢？

 import matplotlib.pyplot as plt %matplotlib inline plt.plot(losses)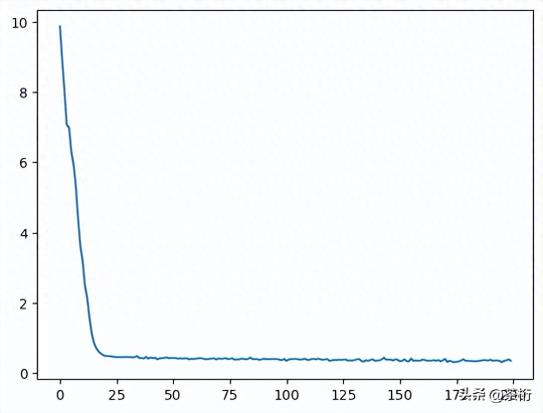

loss持續下降意味著誤差越來越小?方向是對的?測試值更加接近真實值?更精確的說法是，它在逼近最優解，但是效果是不是特別好，還不知道。

接下來這個問題是一個比較復雜的問題，是一個難點：

 -np.sum(y * np.log(yhat) + (1 - y) * np.log(1 - yhat))

這段代碼是我們寫的loss函數， 我們現在來假設有一組數據:

 true_label = np.array([1, 0, 1, 0, 1]) # 二分類

再假設有一個模型，在執行的時候，它會知道咱們做的是一個二分類問題，那么結果就是不是1，就是0。這個時候模型有可能偷懶，那給到的數據就會是隨機的，好吧，開個玩笑，其實就只是因為數據不足造成給到的數據過于隨機：

 predicate_1 = np.array([0.8, 0.7, 0.8, 0.3, 0.8])

然后我們執行算法來拿到結果：

def test_lose(y, yhat):    return -np.sum(y * np.log(yhat) + (1 - y) * np.log(1 - yhat))test_lose(true_label, predicate_1)---2.2300784022072975

現在我們拿到的值為2.23，不過要記得，咱們這只是一個假設值。那這個時候引入我們剛才談到的loss的曲線，loss是持續下降的，當它下降到最低的值的時候依然比這個2.23還要高，那就說明這個模型都還沒有隨機猜測的準確度高。

這個情況其實是經常會遇到的一個問題，你會看到你的的模型一直在下降，下降的非常好，但是一做實際測試的時候效果就特別差。

再換個說法就是，這個模型跑的時候，瞎猜的值都有2.23的準確，但是loss雖然一只在下降，一只下降到了3。雖然loss看起來在下降，但是這整個結果都不是太好。

瞎猜的時候的準確度，loss值，我們稱為這個模型的Baseline。你的值最起碼要比這個好。

所以就如之前所的，loss持續下降意味著模型在向著最優的方向在尋找，但并不意味著結果就會很好，因為有可能連瞎猜都不如。

好，以上是第一點，我們接著來看第二點。

loss一直在下降,但是我們現在想知道的是有多少個label預測對了。先建立兩個變量來分別存儲數據：

true_labels, predicated_labels = [], []...for i in random_test_indices:    ...    true_labels.append(y)    predicated_labels.append(predicate_label)

然后分別獲得了兩組數據，一個是true_labels，一個是predicated_labels。有了這兩組數據之后，我們來定義一個accuracy， 這個是預測的值和相似的值一共有多少個是一樣的。

def accuracy(ytrues, ylabels):    return sum(1 for yt, y1 in zip(ytrues, ylabels) if yt == y1) / len(ytrues)accuracy(true_labels, precicated_labels)---0.89

0.89, 就是說有89%的label都是猜對了。

最早的時候其實只有這一個標記，但這個標記很容易出錯。

假設有一個警察局，要在100個人里邊判斷誰是犯罪分子。現在我們知道有3個是犯罪分子，然后警察說這100個人全部都是犯罪分子。那么現在準確度有多少？

然后又有一個警察站出來說，這100個人都不是犯罪分子，那他的準確度又是多少？

我們現在讓第一個警察是a，第二個警察是b。

警察b有97個標簽都說對了，這會給人一種錯覺，好像他預測的很準確的。但是其實，a和b兩個人都判斷的不準確。那我們這個時候就需要引出一個定義：Precision。

precision也是準確度的意思，和accuracy不同點是，accuracy的對比是對比目標和現有值是否匹配，匹配的就算正確。而precision除了看是否匹配之外，還要目標值，也就是positive。

這里舉個例子說明一下，比如我們去檢測是否有新冠病毒，那么目標是為了檢測出有新館病毒的人，那么呈陽性的人就是我們的positive， 那么我們precision除了預測出有新冠和沒有新冠的人之外，有新冠的人也需要一一對應上，也就是positive要正確。

如果是寫代碼的話，也就是將之前的accuracy拿過來改改就可以直接用了：

def precision(ytrues, yhats):    # 預測標簽是1的里面，正確的比例是多少    positives_pred = [y for y in yhats if y == 1]    return sum(1 for yt, y in zip(ytrues, yhats) if yt == y and y == 1) / len(positives_pred)precision(true_labels, predicated_labels)---0.8333333333333334

先將預測為1，也就是預測呈陽性的目標放到positives_pred中，再來檢測一下在這些預測出來的目標中，預測對的有多少。

除此之外之外，還有一個值叫做recall，它的意思是在實際的positive里，有多少比例被找到了。

def recall(ytrues, yhats):        true_positive = [y for y in ytrues if y == 1]         return sum(1 for yt, y in zip(ytrues, yhats) if yt == y and yt == 1) / len(true_positive)recall(true_labels, predicated_labels)---0.8064516129032258

好，我們再來復盤一下這三個值，一個是accuracy, 一個是precision，一個是recall。

accuracy就是預測值和實際值有多少是一樣的。但是有可能會在實際場景都不是很均衡。

precision是拿到預測后的目標值，然后拿這些目標的實際值去比較看有多大比例是一樣的。

recall是先拿到實際的目標值，然后拿目標預測值比較看有多大比例是一樣的。

根據我們之前說的警察抓壞人的那個假設，我們現在來做一個測試，假設我們現在好人有90個，壞人有10個。

people = [0] * 90 + [1] * 10import randomrandom.shuffle(people)

現在警察a來了，就判斷說：全部都是好人，把他們全部都放了吧。這樣的話，它的accuracy是多少呢？accuracy就是預測的，只要是實際值的那個label就行。我們來看看：

a = [0] * 100accuracy(people, a)---0.9

我們看這個準確度就會很高，這個也能理解，因為警察a將這100個人中的90個好人全部判斷準確了對吧？

讓我們來看看其他兩個：

precision(people, a)---ZeroDivisionError: division by zero======recall(people, a)---0

precision警告我們分母為0，報錯了。那分母為什么為0呢？因為a說了，所有都是好人，那么預測的目標值，也就是分母上的壞人就為0。

而recall呢，結果為0。這是因為分母上的壞人實際值雖然為10，但是預測的目標值，也就是分子上為0。那結果肯定是為0。

本來a的accuracy是0.9，別人還以為準確度很高，結果一個壞人都沒抓住。這肯定不行。

那b的情況又如何呢？之前說過，b說所有的都是壞人，統統抓起來。

b = [1] * 100accuracy(people, b)---0.1========precision(people, b)---0.1=========recall(people, b)---1.0

雖然accuracy和precision都不高，但是似乎目標都被找出來了。頗有一種「寧可錯殺1000，不可放過一個」的感覺。

那以上這些，就是為什么要有這3個非常重要的指標的原因。

好，那下一節課中，我們要來看看關于precition和recall的一個矩陣，這個矩陣呢，將會是我們工作中分析結果常用的。

原文地址：

10. 機器學習-評測指標